题目内容
设函数f(x)=
sin(πx),若存在x0∈(-1,1)同时满足以下条件:
①对任意的x∈R,都有f(x)≤f(x0)成立;
②x02+[f(x0)]2<m2,
则m的取值范围是 .
| ||
| 2 |
①对任意的x∈R,都有f(x)≤f(x0)成立;
②x02+[f(x0)]2<m2,
则m的取值范围是
考点:正弦函数的图象
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:直接利用题中的已知条件建立关系式先求出,对f(x)≤f(x0)成立,只需满f(x)≤f(x0)min即可.由于f(x)=
sin(πx),所以:先求出f(x)的最小值,进一步求出:当x0最小,f(x0)最小时,函数x02+[f(x0)]2<m2,解得:m2≥4,最后求出结果.
| ||
| 2 |
解答:
解:根据题意:①对任意的x∈R,都有f(x)≤f(x0)成立
由于:x0∈(-1,1)
所以:对f(x)≤f(x0)成立,只需满足f(x)≤f(x0)min即可.
由于f(x)=
sin(πx),
所以:f(x0)min=-
由于②x02+[f(x0)]2<m
所以当x0=-
,且f(x0)min=-
求出:m2≥4
进一步求出:m≥2或m≤-2
故答案为:m≥2或m≤-2
由于:x0∈(-1,1)
所以:对f(x)≤f(x0)成立,只需满足f(x)≤f(x0)min即可.
由于f(x)=
| ||
| 2 |
所以:f(x0)min=-
| ||
| 2 |
由于②x02+[f(x0)]2<m
所以当x0=-
| 1 |
| 2 |
| ||
| 2 |
求出:m2≥4
进一步求出:m≥2或m≤-2
故答案为:m≥2或m≤-2
点评:本题考查的知识要点:三角函数的值域,函数的恒成立问题和存在性问题,属于基础题型.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
设Sn是等差数列{an}的前n项和,已知a5=9,S2=4,则a2=( )
| A、1 | B、2 | C、3 | D、5 |
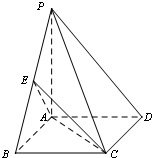 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,点E为PB的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,点E为PB的中点.