题目内容
某人朝正东方走xkm后，向左转150°，然后朝新方向走3km，结果它离出发点恰好
km，那么x等于（ ）
| 3 |
A、
| ||||
B、2
| ||||
C、
| ||||
| D、3 |
考点：解三角形的实际应用
专题：应用题,解三角形
分析：根据题意画出图形，如图所示，在三角形ABC中，利用余弦定理列出关于x的方程，求出方程的解即可得到x的值．
解答：
解：根据题意画出图形，如图所示
在△ABC中，利用余弦定理得：AC2=AB2+BC2-2AB•BCcosB，
即3=9+x2-2×3x×
，
解得：x=
或2
．
故答选：C．
解：根据题意画出图形，如图所示在△ABC中，利用余弦定理得：AC2=AB2+BC2-2AB•BCcosB，
即3=9+x2-2×3x×
| ||
| 2 |
解得：x=
| 3 |
| 3 |
故答选：C．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
设m，n是两条不同的直线，α，β是两个不同的平面．（ ）
| A、若m∥α，n?α，则m∥n |
| B、若m⊥α，n?α，则m⊥n |
| C、若α∥β，m?α，n?β，则m∥n |
| D、若α⊥β，m?α，n?β，则m⊥n |
曲线x2+y2+4x-4y=0关于（ ）
| A、直线x=4对称 |
| B、直线x+y=0对称 |
| C、直线x-y=0对称 |
| D、直线（-4，4）对称 |
把函数y=cosx的图象向左平移
个单位，然后把，图象上的所有点的横坐标缩小到原来的
（纵坐标不变），则所得图形对应的函数解析式为（ ）
| π |
| 4 |
| 1 |
| 2 |
A、y=cos（
| ||||
B、y=cos（2x+
| ||||
C、y=cos（
| ||||
D、y=cos（2x+
|
下列判断正确的是（ ）
A、若向量
| ||||
| B、单位向量都相等 | ||||
| C、共线的向量，若起点不同，则终点一定不同 | ||||
| D、模为0的向量的方向是不确定的 |
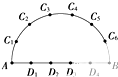如图，在以AB为直径的半圆周上，有异于A、B的六个点C1、C2、C3、C4、C5、C6，直径AB上有异于A、B的四个点D1、D2、D3、D4．以这10个点中的3个点为顶点作三角形可作出多少个（ ）| A、116 | B、128 |
| C、215 | D、98 |
已知双曲线
-
=1的一条渐近线方程为4x+3y=0，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是《函数的应用》的知识结构图，如果要加入“用二分法求方程的近似解”，则应该放在（ ）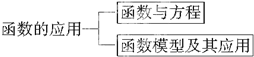
| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |