题目内容
f（x）=a-x2+2x+3（0＜a＜1）的单调增区间是 ．
考点：指数式与对数式的互化
专题：函数的性质及应用
分析：令u=-x2+2x+3=-（x-1）2+4，则u（x）在（1，+∞）单调递减；而函数y=au（0＜a＜1）单调递减，利用复合函数的单调性即可得出．
解答：
解：令u=-x2+2x+3=-（x-1）2+4，则u（x）在（1，+∞）单调递减；
而函数y=au（0＜a＜1）单调递减，
∴f（x）=a-x2+2x+3（0＜a＜1）的单调增区间是（1，+∞）．
故答案为：（1，+∞）．
而函数y=au（0＜a＜1）单调递减，
∴f（x）=a-x2+2x+3（0＜a＜1）的单调增区间是（1，+∞）．
故答案为：（1，+∞）．
点评：本题考查了二次函数、指数函数、复合函数的单调性，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
设
=（
，2sinα），
=（
cosα，
），且
∥
，则锐角α的值为（ ）
| a |
| 1 |
| 3 |
| b |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
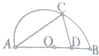如图，某风景区准备美化以快直径为AB的半圆形空地，O为圆心，C为圆周上一点，CD⊥AB于D，已知AB为一假山壁，若以山壁为一边，△ACD内为一喷泉，△ACD外栽种花草，若AB=200米，∠CAB=θ，y=AC+CD．函数y=
的定义域为（ ）
| x(1-x) |
| A、{x|x≥0} |
| B、{x|x≥1} |
| C、{x|x≥1}∪{0} |
| D、{x|0≤x≤1} |
| E、{x|0≤x≤1} |
在等比数列{an}中，若a1，a10是方程3x2-2x-6=0的两根，则a4•a7=（ ）
| A、-6 | ||
| B、-2 | ||
| C、2 | ||
D、
|