题目内容
四个不同的小球放入四个不同的盒子里,求在下列条件下各有多少种不同的放法?
(1)恰有一个盒子里放2个球;
(2)恰有两个盒子不放球.
(1)恰有一个盒子里放2个球;
(2)恰有两个盒子不放球.
考点:计数原理的应用
专题:应用题,排列组合
分析:(1)分两步:首先将四个小球按2,1,1的个数分成三组,再将三组球放入四个盒子中的三个,由分步计数原理,可得结论;
(2)分两类:①将四个小球按3,1的个数分成两组,再将这两组球放入四个盒子中的两个;②将四个小球平均分成两组,再将这两组球放入四个盒子中的两个,由分步计数原理,可得结论.
(2)分两类:①将四个小球按3,1的个数分成两组,再将这两组球放入四个盒子中的两个;②将四个小球平均分成两组,再将这两组球放入四个盒子中的两个,由分步计数原理,可得结论.
解答:
解:(1)分两步:首先将四个小球按2,1,1的个数分成三组,有
种分法;再将三组球放入四个盒子中的三个,有
放法.
由分步计数原理,共有
=144(种).
(2)分两类:①将四个小球按3,1的个数分成两组,再将这两组球放入四个盒子中的两个,有
种放法;②将四个小球平均分成两组,再将这两组球放入四个盒子中的两个,有12
种放法.
由分类计数原理,共有
+12
=84(种).
| C | 2 4 |
| A | 3 4 |
由分步计数原理,共有
| C | 2 4 |
| A | 3 4 |
(2)分两类:①将四个小球按3,1的个数分成两组,再将这两组球放入四个盒子中的两个,有
| C | 3 4 |
| A | 2 4 |
| C | 2 4 |
| A | 2 4 |
由分类计数原理,共有
| C | 3 4 |
| A | 2 4 |
| C | 2 4 |
| A | 2 4 |
点评:本题考查分步计数原理,是一个基础题,解题的过程中注意这种有条件的排列要分步走,先选元素再排列.

练习册系列答案
相关题目
在2008奥运会上两名射击运动员甲、乙在比赛中打出如下成绩:
甲,:8,6,7,8,6,5,9,10,4,7
乙:6,7,7,8,6,7,8,7,9,5,
求出甲乙两人的平均数和方差,并分析甲、乙两人成绩.
甲,:8,6,7,8,6,5,9,10,4,7
乙:6,7,7,8,6,7,8,7,9,5,
求出甲乙两人的平均数和方差,并分析甲、乙两人成绩.
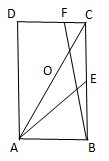 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=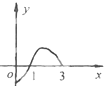 定义在(0,3)上的函数f(x)的图象如图所示
定义在(0,3)上的函数f(x)的图象如图所示