题目内容
在四边形ABCD中，若BC=a，DC=2a，四个角的度数之比为3：7：4：10，求AB的长．
考点：余弦定理
专题：解三角形
分析：根据题意画出图形，由四边形内角和定理及四角之比求出各内角，在三角形BCD中，利用余弦定理求出BD的长，确定出三角形BCD为直角三角形，进而确定出三角形ABD为等腰直角三角形，即AB=
BD，即可求出AB的长．
| 2 |
解答：
解：∵∠A+∠ABC+∠C+∠ADC=360°，四个角的度数之比为3：7：4：10，
∴∠A=45°，∠ABC=105°，∠C=60°，∠ADC=150°，
在△BCD中，BC=a，CD=2a，
由余弦定理得：BD2=a2+4a2-2•a•2a•
=3a2，即BD=
a，
∴△BCD为直角三角形，∠DBC=90°，∠BDC=30°，
在△ABD中，∠A=45°，∠ADB=90°，
∴△ABD为等腰直角三角形，即AD=BD=
AB，
则AB=
BD=
a．
解：∵∠A+∠ABC+∠C+∠ADC=360°，四个角的度数之比为3：7：4：10，∴∠A=45°，∠ABC=105°，∠C=60°，∠ADC=150°，
在△BCD中，BC=a，CD=2a，
由余弦定理得：BD2=a2+4a2-2•a•2a•
| 1 |
| 2 |
| 3 |
∴△BCD为直角三角形，∠DBC=90°，∠BDC=30°，
在△ABD中，∠A=45°，∠ADB=90°，
∴△ABD为等腰直角三角形，即AD=BD=
| ||
| 2 |
则AB=
| 2 |
| 6 |
点评：此题考查了余弦定理，以及解直角三角形，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
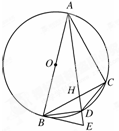如图，AB是⊙O的直径，BE为⊙O的切线，点C为⊙O上不同于A，B的一点，AD为∠BAC的平分线，且分别与BC交于H，与⊙O交于D，与BE交于E，连接BD，CD．