题目内容
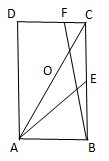如图，在矩形ABCD中，AB=| 2 |
（1）若O是对角线AC的中点，
| AO |
| AE |
| AD |
（2）若
| AE |
| BF |
| 2 |
考点：向量在几何中的应用
专题：平面向量及应用
分析：（1）点E是BC边的中点，O是对角线AC的中点，将
用
，
表示，找到对应的λ，μ；
（2）利用
•
=
，将等式的左边利用矩形的边对应的向量表示，得到关于CF的等式．
| AO |
| AE |
| AD |
（2）利用
| AE |
| BF |
| 2 |
解答：
解：（1）∵点E是BC边的中点，O是对角线AC的中点，
∴
=
=
(
+
)=
(
+
)=
+
，
∴λ=
，μ=
，
∴λ+μ=
；
（2）∵
•
=
，∴
(
+
)(
+
)=
，
∴
(2
+
)(
+
)=
，
展开得
•
+
•
+
•
+
•
=
，
∵AB⊥BC，AB∥CF，AD=BC，AD⊥CF，
∴-
CF+2=
，
∴CF=
，
∴DF=AB-CF=
-
=1．
∴
| AO |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| AE |
| EC |
| 1 |
| 2 |
| AE |
| 1 |
| 2 |
| AD |
| 1 |
| 2 |
| AE |
| 1 |
| 4 |
| AD |
∴λ=
| 1 |
| 2 |
| 1 |
| 4 |
∴λ+μ=
| 3 |
| 4 |
（2）∵
| AE |
| BF |
| 2 |
| 1 |
| 2 |
| AB |
| AC |
| BC |
| CF |
| 2 |
∴
| 1 |
| 2 |
| AB |
| AD |
| BC |
| CF |
| 2 |
展开得
| AB |
| BC |
| AB |
| CF |
| 1 |
| 2 |
| AD |
| BC |
| 1 |
| 2 |
| AD |
| CF |
| 2 |
∵AB⊥BC，AB∥CF，AD=BC，AD⊥CF，
∴-
| 2 |
| 2 |
∴CF=
2-
| ||
|
∴DF=AB-CF=
| 2 |
2-
| ||
|
点评：本题考查了向量的解法的几何意义，以及向量垂直和平行时的数量积的特征．
练习册系列答案
名校课堂系列答案
相关题目
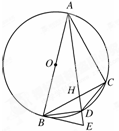如图，AB是⊙O的直径，BE为⊙O的切线，点C为⊙O上不同于A，B的一点，AD为∠BAC的平分线，且分别与BC交于H，与⊙O交于D，与BE交于E，连接BD，CD．