题目内容
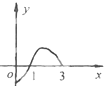定义在（0，3）上的函数f（x）的图象如图所示| a |
| b |
| a |
| b |
考点：平面向量的综合题
专题：平面向量及应用
分析：由已知得x∈（0，1）时f（x）＜0，cosx＞0；x∈[1，
]时，cosx≥0，f（x）≥0；x∈（
，3）时，f（x）＞0，cosx＜0．由此能求出
•
=f（x）cosx＜0的解集．
| π |
| 2 |
| π |
| 2 |
| a |
| b |
解答：
解：∵（0，3）上的函数f（x）的图象如图所示，
=（f（x），0），
=（cosx，0），
∴x∈（0，1）时f（x）＜0，cosx＞0；
x∈[1，
]时，cosx≥0，f（x）≥0；
x∈（
，3）时，f（x）＞0，cosx＜0，
∴
•
=f（x）cosx＜0的解集是（0，1）∪（
，3）．
故答案为：（0，1）∪（
，3）．
| a |
| b |
∴x∈（0，1）时f（x）＜0，cosx＞0；
x∈[1，
| π |
| 2 |
x∈（
| π |
| 2 |
∴
| a |
| b |
| π |
| 2 |
故答案为：（0，1）∪（
| π |
| 2 |
点评：本题考查不等式的解集的求法，是中档题，解题时要认真审题，注意余弦函数性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目