题目内容

双曲线
x2
a2
-
y2
b2
=1（a，b＞0）的渐近线上任意一点P到两个焦点的距离之差的绝对值与2a的大小关系为（　　）
A、恒等于2aB、恒大于2a
C、恒小于2aD、不确定
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：取坐标原点（0，0），可得P到两个焦点的距离之差的绝对值为0＜2a，即可得出结论．
解答： 解：取坐标原点（0，0），可得P到两个焦点的距离之差的绝对值为0＜2a，
故选：C．
点评：本题考查双曲线的性质，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
若x＞0，y＞0且
2
x
+
8
y
=1，则xy的最小值是
 
．
已知函数f（x）=（x2+x-a）e 
x
a
（a＞0）．
（1）当a=1时，求函数f（x）的单调区间；
（2）当a=5时，求f（x）的极值．
已知x，y均为非负数，且
1
x
+
3
y+2
=3，则3x+y的最小值为
 
．
给出下列8种图象的变换方法：
（1）将图象上所有点的横坐标缩短到原来的
1
2
倍（纵坐标不变）．
（2）将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）；
（3）将图象上所有点的纵坐标伸长到原来的3倍（横坐标不变）；
（4）将图象上所有点的纵坐标缩短到原来的
1
3
倍（横坐标不变）；
（5）将图象向左平移
π
3
个单位．
（6）将图象向右平移
π
3
个单位．
（7）将图象向左平移
π
6
个单位．
（8）将图象向右平移个
π
6
单位．
需要且只要用上述3种变换可由函数y=sinx的图象得到y=3sin（2x+
π
3
）的图象，那么这3种变换正确的顺序是
 
（填上一组正确的序号即可）
设f（x）=
x2+2，x≤2
2x，x＞2
，若f（x）=6，则x=（　　）
A、2或3B、-2或3
C、2或3或-2D、±2或±3
sin
19
6
π等于（　　）
A、
1
2
B、
3
2
C、-
1
2
D、-
3
2
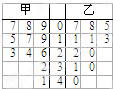某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们每场比赛得分的情况用如图所示的茎叶图表示，若甲运动员的中位数为a，乙运动员的众数为b，则a-b=（　　）
A、4B、6C、8D、12
等差数列{an}满足a2=12，a6=4，则其公差d=（　　）
A、2B、-2C、3D、-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网