题目内容
定义在(0,+∞)上的函数f(x)满足对任意的x1,x2∈(0,+∞)(x1≠x2),有(x2-x1)(f(x2)-f(x1))>0,则满足f(2x-1)<f(
)的x的取值范围是( )
| 1 |
| 3 |
A、(
| ||||
B、[
| ||||
C、(
| ||||
D、[
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据已知条件,由单调递增函数的定义便得到函数f(x)在(0,+∞)上单调递增,所以由f(2x-1)<f(
)得:2x-1<
,且2x-1>0,解不等式即得x的取值范围.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:由(x2-x1)(f(x2)-f(x1))>0,知:x2-x1与f(x2)-f(x1)同号;
∴函数f(x)在(0,+∞)上为增函数;
∴解原不等式得:
,解得
<x<
;
∴x的取值范围是(
,
).
故:C.
∴函数f(x)在(0,+∞)上为增函数;
∴解原不等式得:
|
| 1 |
| 2 |
| 2 |
| 3 |
∴x的取值范围是(
| 1 |
| 2 |
| 2 |
| 3 |
故:C.
点评:考查单调递增函数的定义,并且不要忘了限制2x-1在函数f(x)的定义域内.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
等差数列{an}满足a2=12,a6=4,则其公差d=( )
| A、2 | B、-2 | C、3 | D、-3 |
执行如图所示的程序框图,则输出的结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
过点(3,0),(3,
),的直线的倾斜角为( )
| 3 |
| A、0° | B、30° |
| C、60° | D、90° |
下列函数中既是偶函数,又在(0,+∞)上为增函数的是( )
| A、y=x-2 | ||
| B、y=x-1 | ||
| C、y=x2 | ||
D、y=x
|
已知三棱锥P-ABC的所有顶点都在球O的球面上,AB=5,AC=3,BC=4,PB为球O的直径,PB=10,则这个三棱锥的体积为( )
A、30
| ||
B、15
| ||
C、10
| ||
D、5
|
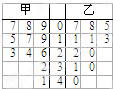 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b=( )
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b=( )