题目内容
已知定义域为R的奇函数f(x),当x≥0时,f(x)=|x-
|-
(a≥0),且对x∈R,恒有f(x+a)≥f(x),则实数a的取值范围是( )
| a |
| a |
| A、[0,2] | ||
| B、{0}∪[2,+∞) | ||
C、[0,
| ||
| D、{0}∪[16,+∞) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:当x≥0时,f(x)=|x-
|-
=
,利用奇函数的性质可得:当x<0时可得f(x)=-f(-x)=
.f(x)的图象如图所示:当x<0时,函数的最大值为
,由于对x∈R,恒有
f(x+a)≥f(x),则a≥3
-(-
),解得即可.
| a |
| a |
|
|
| a |
f(x+a)≥f(x),则a≥3
| a |
| a |
解答:
解:当x≥0时,f(x)=|x-
|-
=
,
设x<0.则-x>0.定义域为R的函数f(x)是奇函数,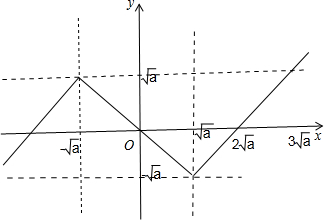
∴f(x)=-f(-x)=
.
f(x)的图象如图所示:
当x<0时,函数的最大值为
,
∵对x∈R,恒有f(x+a)≥f(x),
则a≥3
-(-
),
解得a=0或a≥16.
故选:D.
| a |
| a |
|
设x<0.则-x>0.定义域为R的函数f(x)是奇函数,

∴f(x)=-f(-x)=
|
f(x)的图象如图所示:
当x<0时,函数的最大值为
| a |
∵对x∈R,恒有f(x+a)≥f(x),
则a≥3
| a |
| a |
解得a=0或a≥16.
故选:D.
点评:本题考查了函数的奇偶性、单调性,考查了数形结合的思想方法,考查了推理能力和计算能力,属于较难题.

练习册系列答案
相关题目
f(x)=(m-1)x2+2mx+3为偶函数,则f(x)在区间(2,5)上是( )
| A、减函数 | B、增函数 |
| C、有增有减 | D、增减性不确定 |
已知四边形ABCD满足
•
>0,
•
>0,
•
>0,
•
>0,则四边形为( )
| AB |
| BC |
| BC |
| CD |
| CD |
| DA |
| DA |
| AB |
| A、平行四边形 | B、梯形 |
| C、平面四边形 | D、空间四边形 |
已知集合A={0,1,3},B={2,3},则A∪B=( )
| A、{0,1,2,3} |
| B、{0,1,3} |
| C、{0,2,3} |
| D、{1,2,3} |
等差数列{an}满足a2=12,a6=4,则其公差d=( )
| A、2 | B、-2 | C、3 | D、-3 |
已知三棱锥P-ABC的所有顶点都在球O的球面上,AB=5,AC=3,BC=4,PB为球O的直径,PB=10,则这个三棱锥的体积为( )
A、30
| ||
B、15
| ||
C、10
| ||
D、5
|
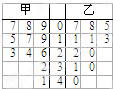 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b=( )
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b=( )