题目内容
数列{an}和{bn}均为等差数列,a1+b1=3,a3+b3=7,则a10+b10的值为( )
| A、20 | B、21 | C、22 | D、23 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:可得数列{an+bn}也为等差数列,设其公差为d,代入已知可得d值,代入通项公式可得.
解答:
解:∵数列{an},{bn}均为等差数列,
∴数列{an+bn}也为等差数列,设其公差为d,
故可得a3+b3=(a1+b1)+2d,即7=3+2d,
解之可得d=2,故a10+b10=a1+b1+9d=3+9×2=21.
故选:B.
∴数列{an+bn}也为等差数列,设其公差为d,
故可得a3+b3=(a1+b1)+2d,即7=3+2d,
解之可得d=2,故a10+b10=a1+b1+9d=3+9×2=21.
故选:B.
点评:本题考查等差数列的性质和求和公式,得出数列{an+bn}也为等差数列是解决问题的关键,属中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
设f(x)=
,若f(x)=6,则x=( )
|
| A、2或3 | B、-2或3 |
| C、2或3或-2 | D、±2或±3 |
直线y=x+m(m为参数)被椭圆
+y2=1截得的弦的长度最大值是( )
| x2 |
| 4 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
当a>0时,下列式子中正确的是( )
A、a
| ||||
B、a
| ||||
C、a
| ||||
D、(a
|
f(x)=(m-1)x2+2mx+3为偶函数,则f(x)在区间(2,5)上是( )
| A、减函数 | B、增函数 |
| C、有增有减 | D、增减性不确定 |
已知集合A={0,1,3},B={2,3},则A∪B=( )
| A、{0,1,2,3} |
| B、{0,1,3} |
| C、{0,2,3} |
| D、{1,2,3} |
过点(3,0),(3,
),的直线的倾斜角为( )
| 3 |
| A、0° | B、30° |
| C、60° | D、90° |
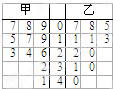 某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b=( )
某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b=( )