题目内容
已知数列{an}满足an+2-2an+1+an=0（n∈N*），且a2=6，a6=-2，则数列{an}的前9项和S9=（ ）
| A、-2 | B、0 | C、4 | D、6 |
考点：数列递推式
专题：等差数列与等比数列
分析：由数列{an}满足an+2-2an+1+an=0，变形为an+2-an+1=an+1-an，可得：数列{an}是等差数列．再利用等差数列的通项公式和前n项和公式即可得出．
解答：
解：∵数列{an}满足an+2-2an+1+an=0，
∴an+2-an+1=an+1-an，
∴数列{an}是等差数列，设公差为d．
∵a2=6，a6=-2，
∴
，解得
．
∴S9=9×8+
×(-2)=0
故选：B．
∴an+2-an+1=an+1-an，
∴数列{an}是等差数列，设公差为d．
∵a2=6，a6=-2，
∴
|
|
∴S9=9×8+
| 9×8 |
| 2 |
故选：B．
点评：本题考查了等差数列的定义、等差数列的通项公式和前n项和公式，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
设f（x）=
，若f（x）=6，则x=（ ）
|
| A、2或3 | B、-2或3 |
| C、2或3或-2 | D、±2或±3 |
sin
π等于（ ）
| 19 |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
直线y=x+m（m为参数）被椭圆
+y2=1截得的弦的长度最大值是（ ）
| x2 |
| 4 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
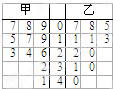某赛季，甲、乙两名篮球运动员都参加了11场比赛，他们每场比赛得分的情况用如图所示的茎叶图表示，若甲运动员的中位数为a，乙运动员的众数为b，则a-b=（ ）f（x）=（m-1）x2+2mx+3为偶函数，则f（x）在区间（2，5）上是（ ）
| A、减函数 | B、增函数 |
| C、有增有减 | D、增减性不确定 |