题目内容
求函数y=
,x∈[-
,
]的值域.
| 1 |
| 2+sinx |
| π |
| 6 |
| 3π |
| 4 |
考点:正弦函数的定义域和值域
专题:计算题,三角函数的图像与性质
分析:根据函数y=sinx在区间[-
,
)上是增函数,在(
,
]上是减函数,求出y=sinx的最大值与最小值,即得所求函数的值域.
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
解答:
解:∵函数y=sinx在区间[-
,
)上是增函数,在(
,
]上是减函数;
∴在x=
时,函数y取得最大值1;
又∵sin(-
)=-
,sin
=
,
∴y=sinx的最小值是-
,
则函数y=
的最小值为
=
,最大值为
=
.
则所求函数的值域为[
,
].
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
∴在x=
| π |
| 2 |
又∵sin(-
| π |
| 6 |
| 1 |
| 2 |
| 3π |
| 4 |
| ||
| 2 |
∴y=sinx的最小值是-
| 1 |
| 2 |
则函数y=
| 1 |
| 2+sinx |
| 1 |
| 2+1 |
| 1 |
| 3 |
| 1 | ||
2-
|
| 2 |
| 3 |
则所求函数的值域为[
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了正弦函数的图象与性质的问题,应用正弦函数在它的定义域上的单调性,求出函数的最值,就可以求出函数的值域,是基础题和易错题.

练习册系列答案
相关题目
已知实数a,b满足1003a+1004b=2006b,997a+1009b=2007a,则a与b的大小关系为( )
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
已知函数f(x)=sin(x+ϕ)+cos(x+ϕ)为偶函数,则ϕ的一个取值为( )
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )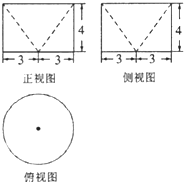

| A、33πcm2 |
| B、42πcm2 |
| C、48πcm2 |
| D、52πcm2 |