题目内容
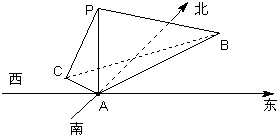 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午9时测得一轮船在海岛北偏东30°,俯角为30°的B处,匀速直行10分钟后,测得该船位于海岛北偏西60°,俯角为45°的C处.从C处开始,该船航向改为正南方向,且速度大小不变,则该船经过10分钟后离开A点的距离为( )| A、1千米 | ||
| B、2千米 | ||
C、
| ||
D、2
|
考点:解三角形的实际应用
专题:应用题,解三角形
分析:设BC交南北轴于点E,延长BC交东西轴于点F,进而利用三角形内角和求得∠FAC和∠FCA,设10分钟后该船到达点D,进而求得CD,在△ACD中运用余弦定理求得AD的长.
解答:
解:设BC交南北轴于点E,延长BC交东西轴于点F,则∠FAC=90°-∠CAE=90°-60°=30°,
∠FCA=180°-60°=120°,
设10分钟后该船到达点D,因为该船向正南航行,所以∠ACD=∠CAE=60°,
10分钟所走的航程是CD=2(千米),
在△ACD中,由余弦定理得:AD2=CD2+AC2-2CD•ACcos∠ACD=4+1-2×2×1×
=3,
∴AD=
(千米)
∴△CAD是直角三角形,∠CAD=90°,而∠FAC=30°,
∴∠FAD=90°-30°=60°.
∴10分钟后该船距离在点A西偏南60°,距离A点
千米处.
故选:C.
∠FCA=180°-60°=120°,
设10分钟后该船到达点D,因为该船向正南航行,所以∠ACD=∠CAE=60°,
10分钟所走的航程是CD=2(千米),
在△ACD中,由余弦定理得:AD2=CD2+AC2-2CD•ACcos∠ACD=4+1-2×2×1×
| 1 |
| 2 |
∴AD=
| 3 |
∴△CAD是直角三角形,∠CAD=90°,而∠FAC=30°,
∴∠FAD=90°-30°=60°.
∴10分钟后该船距离在点A西偏南60°,距离A点
| 3 |
故选:C.
点评:本小题主要考查解三角形的有关知识及空间想象能力,具体涉及到余弦定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知实数a,b满足1003a+1004b=2006b,997a+1009b=2007a,则a与b的大小关系为( )
| A、a<b | B、a>b |
| C、a≤b | D、a≥b |
若某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )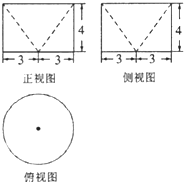

| A、33πcm2 |
| B、42πcm2 |
| C、48πcm2 |
| D、52πcm2 |
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F1的直线分别交双曲线的两条渐近线于点P,Q.若点P是线段F1Q的中点,且QF1⊥QF2,则此双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
将7个红球,6个白球(小球只有颜色的区别)放入5个不同盒子,要求每个盒子中至少红球、白球各一个,则不同的放法共有( )
| A、20种 | B、25种 |
| C、45种 | D、75种 |
已知a>0,b>0,4a+b=1,则ab的最大值是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |