题目内容
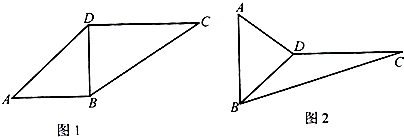
在如图1所示的四边形ABCD中,∠ABD=∠BDC=
,∠C=
,AB=BD=2.现将△ABD沿BD翻折,如图2所示.
(Ⅰ)若二面角A-BD-C为直二面角,求证:AB⊥DC;
(Ⅱ)设E为线段BC上的点,当△ABE为等边三角形时,求二面角A-BD-C的余弦值.
| π |
| 2 |
| π |
| 6 |
(Ⅰ)若二面角A-BD-C为直二面角,求证:AB⊥DC;
(Ⅱ)设E为线段BC上的点,当△ABE为等边三角形时,求二面角A-BD-C的余弦值.

考点:二面角的平面角及求法
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)利用二面角A-BD-C为直二面角,证明AB⊥平面BCD,即可证明AB⊥DC;
(Ⅱ)取BD中点G,连接EG,证明∠ABF为二面角A-BD-C的平面角,再利用余弦定理求求二面角A-BD-C的余弦值.
(Ⅱ)取BD中点G,连接EG,证明∠ABF为二面角A-BD-C的平面角,再利用余弦定理求求二面角A-BD-C的余弦值.
解答:
 (Ⅰ)证明:∵二面角A-BD-C为直二面角,∴平面ABD⊥平面BCD
(Ⅰ)证明:∵二面角A-BD-C为直二面角,∴平面ABD⊥平面BCD
∵AB⊥BD,平面ABD∩平面BCD=BD
∴AB⊥平面BCD
∵DC?平面BCD,∴AB⊥DC;
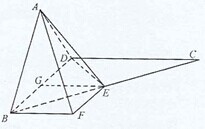
(Ⅱ)∵CB=2BD=2AB,△ABE是等边三角形,
∴E是BC的中点,
取BD中点G,连接EG,
作BF∥GE,且BF=GE,连接EF,AF,
∴四边形EFBG为平行四边形,
∴BF⊥BD,
∵AB⊥BD,
∴∠ABF为二面角A-BD-C的平面角,且BD⊥平面ABF,
∴BD⊥AF,
∵EF∥BD,
∴EF⊥AF,
∵AB=2,
∴Rt△AEF中,EF=BG=1,AE=2,
∴AF=
,
△ABF中,BF=GE=
,
∴cos∠ABF=
=
,
∴二面角A-BD-C的余弦值为
.
 (Ⅰ)证明:∵二面角A-BD-C为直二面角,∴平面ABD⊥平面BCD
(Ⅰ)证明:∵二面角A-BD-C为直二面角,∴平面ABD⊥平面BCD∵AB⊥BD,平面ABD∩平面BCD=BD
∴AB⊥平面BCD
∵DC?平面BCD,∴AB⊥DC;
(Ⅱ)∵CB=2BD=2AB,△ABE是等边三角形,
∴E是BC的中点,
取BD中点G,连接EG,
作BF∥GE,且BF=GE,连接EF,AF,
∴四边形EFBG为平行四边形,
∴BF⊥BD,
∵AB⊥BD,
∴∠ABF为二面角A-BD-C的平面角,且BD⊥平面ABF,
∴BD⊥AF,
∵EF∥BD,
∴EF⊥AF,
∵AB=2,
∴Rt△AEF中,EF=BG=1,AE=2,
∴AF=
| 3 |
△ABF中,BF=GE=
| 3 |
∴cos∠ABF=
| AB2+BF2-AF2 |
| 2AF•BF |
| ||
| 3 |
∴二面角A-BD-C的余弦值为
| ||
| 3 |
点评:本题考查线线垂直,考查空间角,考查学生分析解决问题的能力,正确作出空间角是关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的左右焦点分别为F1,F2,过F1的直线分别交双曲线的两条渐近线于点P,Q.若点P是线段F1Q的中点,且QF1⊥QF2,则此双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2
,则k的取值范围是( )
| 3 |
A、[-
| ||||||||
B、[-∞,-
| ||||||||
C、[-
| ||||||||
D、[-
|