题目内容
9．已知$A=\{x||{x-2}|＜1\}，B=\{y|y=\frac{2x-1}{x+1}，x∈A\}$，则A∩B=（ ）| A． | $（\frac{1}{2}，\frac{5}{4}）$ | B． | $（\frac{7}{4}，3）$ | C． | $（1，\frac{5}{4}）$ | D． | $（\frac{1}{2}，1）$ |
分析 先分别求出集合A和集合B，由此能求出A∩B．
解答 解：∵$A=\{x||{x-2}|＜1\}，B=\{y|y=\frac{2x-1}{x+1}，x∈A\}$，
∴A={x|1＜x＜3}，B={y|$\frac{1}{2}＜x＜\frac{5}{4}$}，
∴A∩B={x|1$＜x＜\frac{5}{4}$}=（1，$\frac{5}{4}$）．
故选：C．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意不等式性质和交集定义的合理运用．
练习册系列答案
相关题目
17．已知复数z1=3-i，z2=1+i，$\overline{{z}_{1}}$是z1的共轭复数，则$\frac{\overline{{z}_{1}}}{{z}_{2}}$=（ ）
| A． | 1+i | B． | 1-i | C． | 2+i | D． | 2-i |
4．已知|$\overrightarrow{OA}$|=1，|$\overrightarrow{OB}$|=2，∠AOB=150°，点C在∠AOB的内部且∠AOC=30°，设$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$，则$\frac{m}{n}$=（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1 |
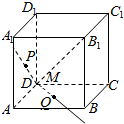如图，M是正方体ABCD-A1B1C1D1对角线AC1上的动点，过点M作垂直于面ACC1A1的直线与正方体表面分别交于P、Q两点，设AM=x，PQ=y，则函数y=f（x）的图象大致为（ ）
