题目内容

2．函数y=$\frac{2}{\sqrt{x-4}}$的值域是（　　）
A．RB．（0，+∞）C．（-∞，4）D．（-∞，4）∪（4，+∞）

分析 由$\sqrt{x-4}＞0$，得$\frac{2}{\sqrt{x-4}}$＞0，即函数的值域为（0，+∞）．

解答 解：由$\sqrt{x-4}＞0$，得$\frac{1}{\sqrt{x-4}}＞0$，
∴$\frac{2}{\sqrt{x-4}}$＞0．
即函数y=$\frac{2}{\sqrt{x-4}}$的值域是（0，+∞）．
故选：B．

点评 本题考查函数值域的求法，体现了极限思想的运用，是基础题．

练习册系列答案
相关题目
12．已知A，B分别为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右顶点，P是C上一点，且直线AP，BP的斜率之积为2，则C的离心率为（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{5}$D．$\sqrt{6}$
13．已知函数f（x）=$\frac{ax+b}{1+{x}^{2}}$是定义在（-1，1）上的奇函数，且f（$\frac{1}{2}$）=$\frac{2}{5}$．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）证明f（x）在（-1，1）上是增函数；
（Ⅲ）若f（x）-3t+1＞0在（-1，0）上恒成立，求t的取值范围．
10．已知函数f（x）=lnx+ax2，g（x）=$\frac{1}{x}$+x+b，且直线y=-$\frac{1}{2}$是函数f（x）的一条切线，求a的值．
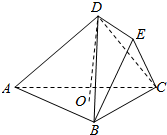17．如图所示，在几何体ABCDE中，AB=BC=CA=EB=EC=2$\sqrt{3}$，DE=$\sqrt{2}$，点D在底面ABC上的射影O为底面三角形ABC的中心，平面BEC⊥平面ABC．
（1）证明：A，D，E，O四点共面；
（2）求几何体ABCDE的体积．
7．用列举法表示A={x|-4＜x＜2，x∈Z}．
14．若z=$\frac{3+2i}{i}$，则|$\overline{z}-1$|等于$\sqrt{10}$．
11．若f（x）=（a-3）x${\;}^{{a}^{2}-3a-2}$既是幂函数又是二次函数，则a的值是（　　）
A．-1B．4C．-1或4D．2
17．已知复数z1=3-i，z2=1+i，$\overline{{z}_{1}}$是z1的共轭复数，则$\frac{\overline{{z}_{1}}}{{z}_{2}}$=（　　）
A．1+iB．1-iC．2+iD．2-i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网