题目内容
1.设角α的终边经过点P(-3a,4a),(a>0),则sinα+2cosα等于( )| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
分析 由题意可得 x=-3a,y=4a,r=5a,可得sinα=$\frac{y}{r}$及cosα=$\frac{x}{r}$值,从而得到sinα+2cosα的值.
解答 解:∵a>0,角α的终边经过点P(-3a,4a),
∴x=-3a,y=4a,r=5a,
∴sinα=$\frac{y}{r}$=$\frac{4}{5}$,cosα=$\frac{x}{r}$=-$\frac{3}{5}$,∴sinα+2cosα=-$\frac{2}{5}$,
故选:C.
点评 本题考查任意角的三角函数的定义,两点间的距离公式的应用,求出sinα和cosα的值是解题的关键.

练习册系列答案
相关题目
11.对任意的实数x,不等式(a2-1)x2+(a-1)x-1<0都成立,则实数a的取值范围是( )
| A. | -$\frac{3}{5}$<a<1 | B. | -$\frac{3}{5}$<a≤1 | C. | -$\frac{3}{5}$≤a≤1 | D. | -$\frac{3}{5}$≤a<1 |
16.在△ABC中,三个内角A、B、C所对的边分别为a、b、c,若内角A、B、C依次成等差数列,且不等式-x2+6x-8>0的解集为{x|a<x<c},则S△ABC等于( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
6.已知{1,2}⊆M?{1,2,3,4},则这样的集合M有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
10.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是( ) 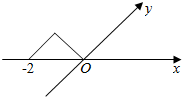

| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |