题目内容
20.在一个棱长为4的正方体内,你认为最多放入的直径为1的球的个数为( )| A. | 64 | B. | 65 | C. | 66 | D. | 67 |
分析 根据球体的特点,最多应该是放5层,确定各层的个数,进一步求出最多可以放入小球的个数即可.
解答 解:根据球体的特点,最多应该是放5层,第一层能放16个;
第2层放在每4个小球中间的空隙,共放9个;第3层继续往空隙放,可放16个;
第4层同第2层放9个;第5层同第1、3层能放16个,
所以最多可以放入小球的个数:16+9+16+9+16=66(个).
故选C.
点评 本题考查的是立体图形,解答此题的关键是找出各层之间的规律再进行解答.

练习册系列答案
相关题目
8.已知椭圆的中心在原点,离心率e=$\frac{1}{2}$,且它的一个焦点与抛物线x2=-4y的焦点重合,则此椭圆的方程为( )
| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B. | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C. | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D. | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
9.现有如下的错误推理:“因为任何复数的平方都大于等于0,而i是复数,所以i2>0,即-1>0”,其错误的原因是( )
| A. | 大前提错误导致结论错误 | B. | 小前提错误导致结论错误 | ||
| C. | 推理形式错误导致结论错误 | D. | 大前提和推理形式都错误导致错误 |
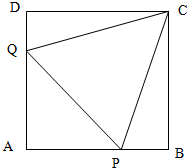 如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.