题目内容
10.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,若$\overrightarrow{a}$•$\overrightarrow{b}$=2.分析 直接根据向量的数量积公式计算即可.
解答 解:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,
$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos60°=2×2×$\frac{1}{2}$=2,
故答案为:2
点评 本题考查了向量的数量积公式,掌握公式是关键,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
10.把函数y=sinx的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图象向右平移$\frac{π}{6}$个单位,这是对应于这个图象的解析式为( )
| A. | $y=sin(2x-\frac{π}{3})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(\frac{x}{2}-\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}-\frac{π}{6})$ |
5.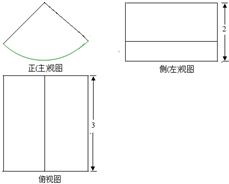 将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
 将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )| A. | 3π+6 | B. | 5π+6 | C. | 3π+12 | D. | 5π+12 |
19.某校周四下午第五、六两节是选修课时间,现有甲、乙、丙三位教师可开课.已知甲、乙教师各自最多可以开设两节课,丙教师最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则丙教师不开课的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
20.在一个棱长为4的正方体内,你认为最多放入的直径为1的球的个数为( )
| A. | 64 | B. | 65 | C. | 66 | D. | 67 |
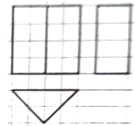 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为32π.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为32π.