题目内容
15.设函数f(x)=|x-1|+|x-a|(a∈R).(Ⅰ)当a=4时,求不等式f(x)≥6的解集;
(Ⅱ)若f(x)≥5对x∈R恒成立,求a的取值范围.
分析 (Ⅰ)当a=4时,把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(Ⅱ)利用绝对值三角不等式求得f(x)的最小值为|a-1|,再根据|a-1|≥5,求得a的取值范围.
解答 解:(Ⅰ)当a=4时,求不等式f(x)≥6,即|x-1|+|x-a|=|x-1|+|x-4|≥6,
∴$\left\{\begin{array}{l}{x<1}\\{1-x+4-x≥6}\end{array}\right.$①,或$\left\{\begin{array}{l}{1≤x≤4}\\{x-1+4-x≥6}\end{array}\right.$ ②,或$\left\{\begin{array}{l}{x>4}\\{x-1+x-4≥6}\end{array}\right.$ ③.
解①求得x≤-$\frac{1}{2}$,解②求得x∈∅,解③求得 x≥$\frac{11}{2}$,
综上可得,不等式的解集为{|x≤-$\frac{1}{2}$,或 x≥$\frac{11}{2}$}.
(Ⅱ)若f(x)≥5对x∈R恒成立,而f(x)=|x-1|+|x-a|≥|x-1-(x-a)|=|a-1|,
∴|a-1|≥5,即a-1≥5,或 a-1≤-5,求得a≥6,或 a≤-4.
点评 本题主要考查绝对值三角不等式,绝对值不等式的解法,函数的恒成立问题,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
5.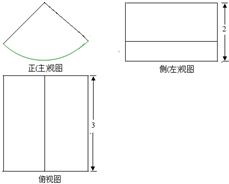 将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
 将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )| A. | 3π+6 | B. | 5π+6 | C. | 3π+12 | D. | 5π+12 |
10.已知函数f(x)=(2ax-lnx)x有两个极值点,则实数a的取值范围是( )
| A. | (0,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (0,+∞) |
20.在一个棱长为4的正方体内,你认为最多放入的直径为1的球的个数为( )
| A. | 64 | B. | 65 | C. | 66 | D. | 67 |
7.抛物线y2=16x的焦点到准线的距离是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
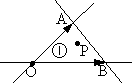 如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )
如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )