题目内容
11.已知f(x)=ax2+bx+c(a≠0),且f(x+1)+f(x-1)=2x2-4x+4,求a、b、c的值.分析 由f(x)=ax2+bx+c,结合条件,运用对应系数相等,得到方程,解方程即可得到.
解答 解:f(x)=ax2+bx+c(a≠0),
则f(x+1)+f(x-1)=a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c
=2ax2+2bx+2a+2c=2x2-4x+4,
∴2a=2,2b=-4,2a+2c=4
∴a=1,b=-2,c=1.
点评 本题考查函数解析式求法,注意运用待定系数法,考查运算能力,属于基础题.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
10.把函数y=sinx的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把图象向右平移$\frac{π}{6}$个单位,这是对应于这个图象的解析式为( )
| A. | $y=sin(2x-\frac{π}{3})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(\frac{x}{2}-\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}-\frac{π}{6})$ |
19.某校周四下午第五、六两节是选修课时间,现有甲、乙、丙三位教师可开课.已知甲、乙教师各自最多可以开设两节课,丙教师最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则丙教师不开课的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
20.在一个棱长为4的正方体内,你认为最多放入的直径为1的球的个数为( )
| A. | 64 | B. | 65 | C. | 66 | D. | 67 |
1.对于R上可导的任意函数f(x),若满足$\frac{3+2x}{f′(x)}$≥0,则有( )
| A. | f(-1)+f(-2)<2f(-$\frac{3}{2}$) | B. | f(-1)+f(-2)>2f(-$\frac{3}{2}$) | C. | f(-1)+f(-2)≤2f(-$\frac{3}{2}$) | D. | f(-1)+f(-2)≥2f(-$\frac{3}{2}$) |
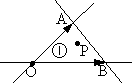 如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )
如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )