题目内容
8.已知椭圆的中心在原点,离心率e=$\frac{1}{2}$,且它的一个焦点与抛物线x2=-4y的焦点重合,则此椭圆的方程为( )| A. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ | B. | $\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$ | C. | ${x}^{2}+\frac{{y}^{2}}{2}=1$ | D. | $\frac{{x}^{2}}{6}+\frac{{y}^{2}}{8}=1$ |
分析 抛物线x2=-4y的焦点为(0,-1),为椭圆的一个焦点.因此可设椭圆的标准方程为:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0).则c=1,$\frac{c}{a}=\frac{1}{2}$,a2=b2+c2,联立解得即可得出.
解答 解:抛物线x2=-4y的焦点为(0,-1),为椭圆的一个焦点.
因此可设椭圆的标准方程为:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0).
则c=1,$\frac{c}{a}=\frac{1}{2}$,a2=b2+c2,
联立解得a=2,b2=3.
∴此椭圆的标准方程为:$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}$=1.
故选;B.
点评 本题考查了椭圆与抛物线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.某校周四下午第五、六两节是选修课时间,现有甲、乙、丙三位教师可开课.已知甲、乙教师各自最多可以开设两节课,丙教师最多可以开设一节课.现要求第五、六两节课中每节课恰有两位教师开课(不必考虑教师所开课的班级和内容),则丙教师不开课的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $\frac{1}{9}$ |
20.在一个棱长为4的正方体内,你认为最多放入的直径为1的球的个数为( )
| A. | 64 | B. | 65 | C. | 66 | D. | 67 |
18.已知函数f(x)=x3-6x2+12x+a(a∈R),则函数f(x)的极值点的个数为( )
| A. | 0 | B. | 1 | ||
| C. | 2 | D. | 与实数a的取值有关 |
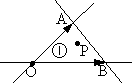 如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )
如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( ) 已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.
已知直线l:4x+3y+15=0,半径为3的⊙C与l相切,圆心C在x轴上且在直线l的右上方.