题目内容
已知A（2，0），B（0，2），C（cosα，sinα），（0＜α＜π）．
（1）若|
+
|=
（O为坐标原点），求
与
的夹角；
（2）若
⊥
，求sinα-cosα的值．
（1）若|
| OA |
| OC |
| 7 |
| OB |
| OC |
（2）若
| AC |
| BC |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：（1）用坐标表示
、
，由|
+
|=
，求出α的值，从而得
，再求得
与
的夹角；
（2）用坐标表示
、
，由
⊥
，得
•
=0，求出sinα+cosα的值，从而求得sinα-cosα的值．
| OA |
| OC |
| OA |
| OC |
| 7 |
| OC |
| OB |
| OC |
（2）用坐标表示
| AC |
| BC |
| AC |
| BC |
| AC |
| BC |
解答：
解：（1）∵
=（2，0），
=（cosα，sinα），
∴
+
=（2，0）+（cosα，sinα）=（2+cosα，sinα），
∴|
+
|=
=
=
，
解得cosα=
，
又∵0＜α＜π，
∴α=
，
∴sinα=
，
∴
=（
，
），又
=（0，2），
设
与
的夹角为θ，则0＜θ＜π；
∴cosθ=
=
=
，
∴θ=
．
（2）∵
=（-2+cosα，sinα），
=（cosα，-2+sinα），
且
⊥
，
∴
•
=0，
即（-2+cosα）cosα+（-2+sinα）sinα=0，
∴-2conα-2sinα+1=0，
∴sinα+cosα=
，
∴1+2sinαcosα=
，
∴2sinαcosα=-
，
又0＜α＜π，
∴cosα＜0，
∴sinα-cosα=
=
=
．
| OA |
| OC |
∴
| OA |
| OC |
∴|
| OA |
| OC |
| (2+cosα)2+(sinα)2 |
| 5+4cosα |
| 7 |
解得cosα=
| 1 |
| 2 |
又∵0＜α＜π，
∴α=
| π |
| 3 |
∴sinα=
| ||
| 2 |
∴
| OC |
| 1 |
| 2 |
| ||
| 2 |
| OB |
设
| OB |
| OC |
∴cosθ=
| ||||
|
|
0×
| ||||||||||
|
| ||
| 2 |
∴θ=
| π |
| 6 |
（2）∵
| AC |
| BC |
且
| AC |
| BC |
∴
| AC |
| BC |
即（-2+cosα）cosα+（-2+sinα）sinα=0，
∴-2conα-2sinα+1=0，
∴sinα+cosα=
| 1 |
| 2 |
∴1+2sinαcosα=
| 1 |
| 4 |
∴2sinαcosα=-
| 3 |
| 4 |
又0＜α＜π，
∴cosα＜0，
∴sinα-cosα=
| (sinα+cosπ)2-4sinαcosα |
(
|
| ||
| 2 |
点评：本题考查了平面向量数量积的运算以及三角函数的运算问题，是综合性题目．
练习册系列答案
相关题目
已知两数-2与-5，则这两数的等比中项是（ ）
A、
| ||
B、-
| ||
C、±
| ||
| D、不存在 |
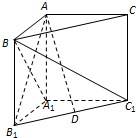如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1．