题目内容
已知函数f(x)=cosx(
cosx-sinx)-
.求:
(Ⅰ)函数y=f(x)的对称轴方程;
(Ⅱ)函数y=f(x)在区间[0,
]上的最值.
| 3 |
| ||
| 2 |
(Ⅰ)函数y=f(x)的对称轴方程;
(Ⅱ)函数y=f(x)在区间[0,
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:计算题,三角函数的图像与性质
分析:(Ⅰ)利用三角函数中的恒等变换,可求得f(x)=-sin(2x-
),利用正弦函数的对称性可求得函数y=f(x)的对称轴方程;
(Ⅱ)0≤x≤
⇒2x-
∈[-
,
]⇒-
≤sin(2x-
)≤1,从而可求函数y=f(x)在区间[0,
]上的最值.
| π |
| 3 |
(Ⅱ)0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:
(Ⅰ)f(x)=
cos2x-sinxcosx-
=
•
-
sin2x-
=
cos2x-
sin2x
=-sin(2x-
),
令2x-
=kπ+
(k∈Z),
解得x=
+
(k∈Z),
故y=f(x)的对称轴方程为x=
+
(k∈Z).
(Ⅱ)由0≤x≤
⇒2x-
∈[-
,
],
∴-
≤sin(2x-
)≤1,
∴-1≤-sin(2x-
)≤
,
∴ymin=-1,ymax=
.
| 3 |
| ||
| 2 |
=
| 3 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=-sin(2x-
| π |
| 3 |
令2x-
| π |
| 3 |
| π |
| 2 |
解得x=
| kπ |
| 2 |
| 5π |
| 12 |
故y=f(x)的对称轴方程为x=
| kπ |
| 2 |
| 5π |
| 12 |
(Ⅱ)由0≤x≤
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴-1≤-sin(2x-
| π |
| 3 |
| ||
| 2 |
∴ymin=-1,ymax=
| ||
| 2 |
点评:本题考查三角函数中的恒等变换,考查正弦函数的对称性与单调性,考查运算求解能力,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
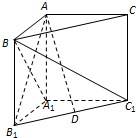 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1.