题目内容
1.过点(3,2)的直线l与x轴的正半轴,y轴的正半轴分别交于A,B两点,当△AOB的面积最小时,求直线l的方程及△AOB面积.分析 设A(a,0),B(0,b),可得直线l的方程为::$\frac{x}{a}$+$\frac{y}{b}$=1.把点P(3,2)代入利用基本不等式的性质、三角形面积计算公式即可得出.
解答 解:设A(a,0),B(0,b),则直线l的方程为:$\frac{x}{a}$+$\frac{y}{b}$=1.
把点P(3,2)代入可得:$\frac{3}{a}$+$\frac{2}{b}$=1.(a,b>0).
∴1≥2$\sqrt{\frac{3}{a}•\frac{2}{b}}$,化为ab≥24,当且仅当a=6,b=4时取等号.
∴S△AOB=$\frac{1}{2}$ab≥12,l的方程为:$\frac{x}{6}$+$\frac{y}{4}$=1,即4x+6y-24=0
点评 本题考查了截距式、基本不等式的性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.三个数0.76,60.7,log0.76的大小关系为( )
| A. | 0.76<log0.76<60.7 | B. | log0.76<0.76<60.7 | ||
| C. | log0.76<60.7<0.76 | D. | 0.76<60.7<log0.76 |
10.已知$tan(α+β)=\frac{1}{2},tanβ=\frac{1}{3}$,则$tan(α-\frac{π}{4})$=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
11.已知程序框图如图所示,当输入x=2时,输出结果为( )


| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
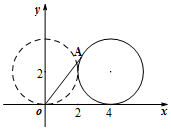 如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).
如图,半径为2的圆圆心的初始位置坐标为(0,2),圆上一点A坐标为(0,0).圆沿x轴正向滚动,当圆滚动到圆心位于(4,2)时,A点坐标为(4-2sin2,2-2cos2).