题目内容
袋中有大小相同的五个球,偏号分别为1,2,3,4,5,从袋中每次任取一个球,记下其编号.若所取球的编号为奇数,把该球编号改为2后放回袋中继续取球,若所取球的编号为偶数,则停止取球.
(Ⅰ)求“第三次取球后停止取球”的概率;
(Ⅱ)若第一次取到奇数,记第二次与第一次取球的编号之和为ζ,求ζ的分布列和数学期望.
(Ⅰ)求“第三次取球后停止取球”的概率;
(Ⅱ)若第一次取到奇数,记第二次与第一次取球的编号之和为ζ,求ζ的分布列和数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:综合题,概率与统计
分析:(Ⅰ)利用相互独立事件同时发生的概率计算公式能求“第三次取球后停止取球”的概率;
(Ⅱ)由已知条件推导出ζ的可能取值,分别求出相对应的概率,由此能求出ζ的分布列和数学期望.
(Ⅱ)由已知条件推导出ζ的可能取值,分别求出相对应的概率,由此能求出ζ的分布列和数学期望.
解答:
解:(Ⅰ)记“第三次取球后才停止取球”为事件A.
∴第一次取到奇数球的概率为
,第二次取球时袋中有2个奇数,
∴第二次取到奇数球的概率为
,第三次取球时袋中有2个偶数球,
而这三次取球相互独立,
∴P(A)=
×
×
=
;
(Ⅱ)若第一次取到1时,第二次取球时袋中有编号为2,2,3,4,5的五个球;
若第一次取到3时,第二次取球时袋中有编号为1,2,2,4,5的五个球;
第一次取到5时,第二次取球时袋中有编号为1,2,2,3,4的五个球.
∴ζ的可能取值为3,4,5,6,7,8,9
P(ζ=3)=
×
=
,P(ζ=4)=
×
+
×
=
,P(ζ=5)=
×
+
×
=
,
P(ζ=6)=
×
+
×
=
,P(ζ=7)=
×
+
×
=
,P(ζ=8)=
×
+
×
=
,
P(ζ=9)=
×
=
,
∴ζ的分布列为
数学期望Eζ=3×
+4×
+5×
+6×
+7×
+8×
+9×
=
.
∴第一次取到奇数球的概率为
| 3 |
| 5 |
∴第二次取到奇数球的概率为
| 2 |
| 5 |
而这三次取球相互独立,
∴P(A)=
| 3 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 24 |
| 125 |
(Ⅱ)若第一次取到1时,第二次取球时袋中有编号为2,2,3,4,5的五个球;
若第一次取到3时,第二次取球时袋中有编号为1,2,2,4,5的五个球;
第一次取到5时,第二次取球时袋中有编号为1,2,2,3,4的五个球.
∴ζ的可能取值为3,4,5,6,7,8,9
P(ζ=3)=
| 1 |
| 3 |
| 2 |
| 5 |
| 2 |
| 15 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
| 2 |
| 15 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 15 |
P(ζ=6)=
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
| 2 |
| 15 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 15 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
| 2 |
| 15 |
P(ζ=9)=
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 15 |
∴ζ的分布列为
| ζ | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||||
| P |
|
|
|
|
|
|
|
| 2 |
| 15 |
| 2 |
| 15 |
| 3 |
| 15 |
| 2 |
| 15 |
| 3 |
| 15 |
| 2 |
| 15 |
| 1 |
| 15 |
| 87 |
| 15 |
点评:本题考查求离散型随机变量的分布列以及数学期望等有关知识.求出随机变量ζ所有可能的取值的概率,是解题的难点.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
△ABC中,A>B是sinB<sinA成立的( )条件.
| A、必要不充分 | B、充分不必要 |
| C、充要 | D、不充分不必要 |
函数y=
sin(2x-
)的图象可以看作是把函数y=
sin2x的图象( )
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
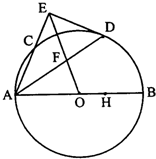 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.