题目内容
设函数f(x)=|lnx|,则下列结论中正确的是( )
A、f(1)<f(
| ||
B、f(
| ||
C、f(e)<f(1)<f(
| ||
D、f(e)<f(
|
考点:对数函数的图像与性质,函数的图象与图象变化
专题:函数的性质及应用
分析:直接将x=1,x=
,x=e代入函数表达式,求出函数值比较即可.
| 1 |
| 2 |
解答:
解:∵f(1)=|ln1|=0,
f(
)=|ln
|=|-ln2|=ln2,
f(e)=|lne|=lne,
∴f(1)<f(
)<f(e),
故答案选:A.
f(
| 1 |
| 2 |
| 1 |
| 2 |
f(e)=|lne|=lne,
∴f(1)<f(
| 1 |
| 2 |
故答案选:A.
点评:本题是关于对数函数的问题,计算过程中小心出错,是一道基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
函数f(x)=4sin(4x-
)是( )
| 5π |
| 2 |
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
函数f(x)=
+lg
的定义域是( )
| ||
| x-3 |
| 4-x |
| A、(2,4) |
| B、(3,4) |
| C、(2,3)∪(3,4] |
| D、[2,3)∪(3,4) |
 已知正四面体的俯视图如图所示,其中ABCD是边长为2的正方形,则这个正四面体的体积为( )
已知正四面体的俯视图如图所示,其中ABCD是边长为2的正方形,则这个正四面体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知sinα+cosα=-
,求tanα+
=( )
| 2 |
| 1 |
| tanα |
| A、2 | B、1 | C、-1 | D、-2 |
△ABC中,A>B是sinB<sinA成立的( )条件.
| A、必要不充分 | B、充分不必要 |
| C、充要 | D、不充分不必要 |
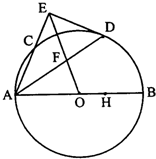 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.