题目内容
10．已知函数f（x）=lnx+$\frac{1}{2}$ax2-（a+1）x+1在x=1处取得极小值，则实数a的取值范围是a＞1．分析 求出函数的导数，得到函数的极值点，根据函数在x=1处取得极小值，求出a的范围即可．
解答 解：f（x）的定义域是（0，+∞），
∵f（x）=lnx+$\frac{1}{2}$ax2-（a+1）x+1，
∴f′（x）=$\frac{1}{x}$+ax-（a+1）=$\frac{（ax-1）（x-1）}{x}$，
令f′（x）=0，解得：x=$\frac{1}{a}$或x=1，
若f（x）在x=1处取得极小值，
则0＜$\frac{1}{a}$＜1，解得：a＞1，
故答案为：a＞1．
点评 本题考查了函数的单调性、极值问题，考查导数的应用，是一道中档题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
20．
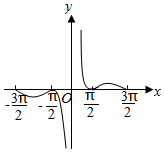已知函数f（x）的图象如图所示，则f（x）的解析式可能是（ ）
已知函数f（x）的图象如图所示，则f（x）的解析式可能是（ ）| A． | $\frac{|cos3x|}{x}$ | B． | $\frac{1+cos2x}{2x}$ | ||
| C． | $\frac{（4{x}^{2}-{π}^{2}）（4{x}^{2}-9{π}^{2}）}{{x}^{5}}$ | D． | $\frac{|sin2x|}{x}$ |