=( )A．2B．1C．-1D．-2 题目和参考答案——青夏教育精英家教网—

题目内容

5．（1+tan20°）（1+tan25°）=（　　）

A．

B．

C．

-1

D．

-2

分析把所给的式子展开，利用两角和的正切公式，化简可得结果．

解答解：（1+tan20°）（1+tan25°）=1+tan20°+tan25°+tan20°tan25°=1+tan（20°+25°）•（1-tan20°•tan25°）+tan20°tan25°
=1+1-tan20°•tan25°）+tan20°•tan25°=2，
故选：A．

点评本题主要考查两角和的正切公式的变形应用，属于基础题．

练习册系列答案

16．设l，m，n表示三条直线，α，β，γ表示三个平面，则下列命题中不成立的是（　　）

	A．	若m?α，n?α，m∥n，则n∥α
	B．	若α⊥γ，α∥β，则β⊥γ
	C．	若m?β，n是l在β内的射影，若m⊥l，则m⊥n
	D．	若α⊥β，α∩β=m，l⊥m，则l⊥β

13．某种饮料每箱装6瓶，库存23箱未开封的饮料，现欲对这种饮料进行质量检测，工作人员需从中随机取出10瓶，若采用系统抽样法，则要剔除的饮料瓶数是（　　）

20．

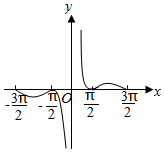已知函数f（x）的图象如图所示，则f（x）的解析式可能是（　　）

	A．	$\frac{\|cos3x\|}{x}$		B．	$\frac{1+cos2x}{2x}$
	C．	$\frac{（4{x}^{2}-{π}^{2}）（4{x}^{2}-9{π}^{2}）}{{x}^{5}}$		D．	$\frac{\|sin2x\|}{x}$

10．已知p：-1＜x＜0，q：m-1＜x＜m+1，若p是q的充分条件，则m的取值范围是[-1，0]．

17．已知实数x，y满足$\left\{\begin{array}{l}{y≥0}\\{x-y≥0}\\{2x-y-2≥0}\end{array}\right.$，则ω=$\frac{y-1}{x+1}$的取值范围是（　　）

A．

[-1，$\frac{1}{3}$]

B．

[-$\frac{1}{2}$，$\frac{1}{3}$]

14．等差数列{a_n}的前n项和为S_n，若S₁₀=80，a₄=5，则a₁₃=（　　）

15．已知函数f（x）=lnx+ax²-ax，其中a∈R．
（1）当a=0时，求函数f（x）在x=1处的切线方程；
（2）若函数f（x）在定义域上有且仅有一个极值点，求实数a的取值范围；
（3）若对任意x∈[1，+∞），f（x）≥0恒成立，求实数a的取值范围．

试题分类