题目内容
11．下列四个判断：①某校高三一班和高三二班的人数分别是m，n，某次测试数学平均分分别是a，b，则这两个班的数学平均分为$\frac{a+b}{2}$；
②10名工人某天生产同一零件的件数分别是15，17，14，10，15，17，17，16，14，12，设其平均数为a，中位数为b，众数为c，则有c＞a＞b；
③从总体中抽取的样本为$（{x_1}，y{_1}），（x{_2}，{y_2}），…，（{x_n}，{y_n}），若记\overline x=\frac{1}{n}\sum_{i=1}^n{{x_i}，\overline y=\frac{1}{n}}\sum_{i=1}^n{\;}{y_i}$，则回归直线$\widehaty=\widehatbx+\widehata$必过点（$\overline x，\overline y$）
④已知ξ服从正态分布N（0，σ2），且P（-2≤ξ≤0）=4，则P（ξ＞2）=0.2
其中正确的个数有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
分析 由平均数的定义，计算即可判断①；
运用平均数、中位数和众数的定义，即可判断②；
由线性回归直线必过样本中心点，即可判断③；
由ξ服从正态分布N（0，σ2），即曲线关于y轴对称，求得P（ξ＜-2），即可判断④．
解答 解：①由题意可得这两个班的数学平均分为$\frac{ma+nb}{m+n}$，故①错；
②由题意可得a=$\frac{1}{10}$（15+17+14+10+15+17+17+16+14+12）=14.7，b=15，c=17，
即有c＞b＞a，故②错；
③由线性回归方程的特点，可得回归直线$\widehaty=\widehatbx+\widehata$必过样本中心点（$\overline x，\overline y$），故③对；
④已知ξ服从正态分布N（0，σ2），且P（-2≤ξ≤0）=0.4，则P（ξ＜-2）=0.5-0.4=0.1，
则P（ξ＞2）=P（ξ＜-2）=0.1，故④错．
故选：D．
点评 本题考查命题的真假判断，考查平均数、中位数和众数，以及线性回归直线和正态分布的特点，考查判断能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
6．复数$z=\frac{2+4i}{1+i}$（i为虚数单位）在复平面内对应点的坐标是（ ）
| A． | （3，1） | B． | （-1，3） | C． | （3，-1） | D． | （2，4） |
16．设l，m，n表示三条直线，α，β，γ表示三个平面，则下列命题中不成立的是（ ）
| A． | 若m?α，n?α，m∥n，则n∥α | |
| B． | 若α⊥γ，α∥β，则β⊥γ | |
| C． | 若m?β，n是l在β内的射影，若m⊥l，则m⊥n | |
| D． | 若α⊥β，α∩β=m，l⊥m，则l⊥β |
20．
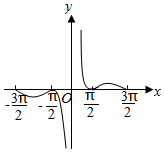已知函数f（x）的图象如图所示，则f（x）的解析式可能是（ ）
已知函数f（x）的图象如图所示，则f（x）的解析式可能是（ ）| A． | $\frac{|cos3x|}{x}$ | B． | $\frac{1+cos2x}{2x}$ | ||
| C． | $\frac{（4{x}^{2}-{π}^{2}）（4{x}^{2}-9{π}^{2}）}{{x}^{5}}$ | D． | $\frac{|sin2x|}{x}$ |