题目内容
已知(x-
)6的展开式中常数项为-160,则常数a=( )
| 2a |
| x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
考点:二项式定理的应用
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项,再根据常数项等于-160求得实数a的值.
解答:
解:由于(x-
)6的展开式的通项公式为Tr+1=
•(-2a)r•x6-2r,
零6-2r=0,求得r=3,可得展开式的常数项为
•(-8a3)=-160a3,
再根据展开式中常数项为-160,可得-160a3=-160,求得a=1,
故选:C.
| 2a |
| x |
| C | r 6 |
零6-2r=0,求得r=3,可得展开式的常数项为
| C | 3 6 |
再根据展开式中常数项为-160,可得-160a3=-160,求得a=1,
故选:C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
设命题p:曲线y=e-x在点(-1,e)处的切线方程:y=-ex;命题q:函数y=sinx+
(0<x<π)值域为[4,+∞),则下列判断正确的是( )
| 4 |
| sinx |
| A、“p∨q”为真 |
| B、“¬p∨q”为真 |
| C、“¬p∧q”为真 |
| D、“¬p∧¬q”为真 |
已知|
|=|
|=2,
在
上的投影为-1,则向量
与向量
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、150° | B、120° |
| C、60° | D、30° |
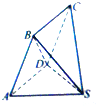 如图,在几何体S-ABCD中,平面ABCD⊥平面SAD,四边形ABCD为平行四边形,且AB=3,AD=2
如图,在几何体S-ABCD中,平面ABCD⊥平面SAD,四边形ABCD为平行四边形,且AB=3,AD=2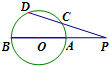 如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=
如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=