题目内容
设a=0.32，b=20.3，c=log20.3，则a，b，c三者的大小关系是 ．（用“＜”连接）
考点：指数函数的图像与性质,对数的运算性质
专题：函数的性质及应用
分析：根据对数函数和指数函数比较a，b，c与0，1的关系，即可得到答案．
解答：
解：∵0＜0.32＜1，20.3＞1，log20.3＜0，
∴c＜a＜b，
故答案为：c＜a＜b，
∴c＜a＜b，
故答案为：c＜a＜b，
点评：本题主要考查了指数函数和对数函数的图象和性质，关键是找到和0，1和关系，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，点D是边BC的中点，点E是线段AD的中点，连接CE交边AB于点F，若
=λ
，则实数λ的值是（ ）
| AB |
| AF |
A、
| ||
| B、4 | ||
C、
| ||
| D、3 |
若loga（π-3）＜logb（π-3）＜0，a，b为不等于1的正数，则下列不等式中正确（ ）
| A、b＞a＞1 |
| B、a＜b＜1 |
| C、a＞b＞1 |
| D、b＜a＜1 |
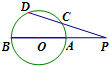如图所示，AB是半径等于3的⊙O的直径，CD是⊙O的弦，BA，DC的延长线交于点P，若PA=4，PC=5，则DC=