题目内容
向量
=(1,-2),
=(2,1),则( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量的坐标运算,数量积表示两个向量的夹角
专题:平面向量及应用
分析:运用数量积的坐标表示,求出两向量的数量积,再由夹角公式,判断两向量的位置关系.
解答:
解:∵向量
=(1,-2),
=(2,1),
∴
•
=1×2+(-2)×1=0,
∴夹角的余弦为0,
∴
⊥
.
故选B.
| a |
| b |
∴
| a |
| b |
∴夹角的余弦为0,
∴
| a |
| b |
故选B.
点评:本题主要考查运用两向量数量积求夹角,考查数量积的坐标表示,注意区别两向量共线与垂直的坐标表示.

练习册系列答案
相关题目
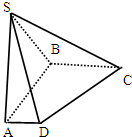 如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,则点B到平面SCD的距离为( )
如图所示,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,且SA=AB=BC=2,AD=1,则点B到平面SCD的距离为( )A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
下列函数中,在(0,+∞)上为增函数的是( )
A、y=(
| ||
B、y=log
| ||
C、y=
| ||
| D、y=x3 |
数列{an}中,已知a1=5,an=an-1+3(n≥2),则数列{an}的第三项为( )
| A、5 | B、8 | C、11 | D、14 |
在棱长为a的正方体ABCD-A1B1C1D1中,错误的是( )
| A、直线A1B和直线AC所成角的大小为60° | ||
| B、直线AC∥平面DA1C1 | ||
C、二面角B-AB1-C的大小是arctan
| ||
| D、直线A1B1到平面ABC1D1的距离为a |
若a<b<0,则下列不等式成立的是( )
| A、a2<b2 |
| B、a2≤b2 |
| C、a-b>0 |
| D、|a|>|b| |
已知向量
=(1,0),
=(-
,
),则
与
的夹角为( )
| a |
| b |
| 1 |
| 2 |
| ||
| 2 |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
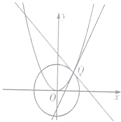 如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=
如图,抛物线C:x2=2py与圆O:x2+y2=1在第一象限的交点为Q,圆O和抛物线C在点Q处的切线的斜率分别为k1,k2,若k1+k2=1,则p=