题目内容
若函数f(x)=|x+a|-
有两个零点,则实数a的取值范围 .
| 1-x2 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数有零点就是方程有解,再利用根的判别式求出参数a的范围即可.
解答:
解:f(x)=|x+a|-
有两个零点,
∴f(x)=0,即|x+a|-
=0有两个不相等的实数根,
∴2x2+2ax+a2-1=0有两个不相等的实数根
∴△>0
即4a2-8(a2-1)>0
解得,-
<a<
.
故答案为:(-
,
)
| 1-x2 |
∴f(x)=0,即|x+a|-
| 1-x2 |
∴2x2+2ax+a2-1=0有两个不相等的实数根
∴△>0
即4a2-8(a2-1)>0
解得,-
| 2 |
| 2 |
故答案为:(-
| 2 |
| 2 |
点评:本题主要考查了函数的零点的问题,关键利用根的判别式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
向量
=(1,-2),
=(2,1),则( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
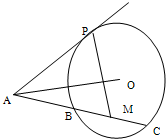 (几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为
(几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为