题目内容
下列函数中，在（0，+∞）上为增函数的是（ ）
A、y=（
| ||
B、y=log
| ||
C、y=
| ||
| D、y=x3 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：由条件利用基本初等函数的单调性逐一判断各个选项是否正确，从而得出结论．
解答：
解：由于y=（
）x 在（0，+∞）上为减函数，故排除A；
由于y=log
x 在（0，+∞）上为减函数，故排除B；
由于y=
在（0，+∞）上为减函数，故排除C；
由于y=x3在（0，+∞）上为增函数，故满足条件，
故选：D．
| 1 |
| 2 |
由于y=log
| 1 |
| 2 |
由于y=
| 1 |
| x |
由于y=x3在（0，+∞）上为增函数，故满足条件，
故选：D．
点评：本题主要考查基本初等函数的单调性，属于基础题．
练习册系列答案
相关题目
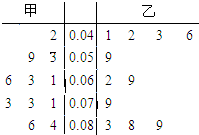PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据（单位：毫克/每立方米）列出的茎叶图，如图，则甲、乙两地所测数据的中位数较低的是（ ）| A、甲 | B、乙 |
| C、甲乙相等 | D、无法确定 |
5名学生与2名教师排成一排拍照，2名教师相邻且不排在两端，共有不同的排法种数为（ ）
| A、1440 | B、960 |
| C、720 | D、480 |
向量
=（1，-2），
=（2，1），则（ ）
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直二面角α-l-β，点A∈α，B∈β，A、B到棱l的距离相等，直线AB与平面β所成的角为30°，则AB与棱l所成的角的余弦是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| cos2600° |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
复数
的共轭复数对应的点在复平面的（ ）
| 5 |
| i-2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |