题目内容
若a<b<0,则下列不等式成立的是( )
| A、a2<b2 |
| B、a2≤b2 |
| C、a-b>0 |
| D、|a|>|b| |
考点:不等关系与不等式
专题:不等式的解法及应用
分析:利用不等式的基本性质即可得出.
解答:
解:∵a<b<0,∴-a>-b>0,
∴|a|>|b|.
故选:D.
∴|a|>|b|.
故选:D.
点评:本题考查了不等式的基本性质,属于基础题.

练习册系列答案
相关题目
向量
=(1,-2),
=(2,1),则( )
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知椭圆C:
+
=1(a>0,b>0)的右焦点为F,椭圆C与过原点的直线相交于A、B两点,连接AF、BF,若|AB|=8,|BF|=4,且cos∠ABF=
,则椭圆C的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| cos2600° |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
过椭圆
+y2=1(a>1)的右焦点F作相互垂直的两条弦AB和CD,若|AB|+|CD|的最小值为2
,则椭圆的离心率e=( )
| x2 |
| a2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
长方体的表面积是24,所有棱长的和是24,则对角线的长是( )
A、
| ||
| B、4 | ||
C、3
| ||
D、2
|
已知m、n、l为直线,α、β、γ为平面,下列命题为真命题的是( )
| A、若m∥α,m∥β,则α∥β |
| B、若m?α,n?β,α⊥β,则m⊥n |
| C、若l⊥n,l⊥m,m?α,n?α,则l⊥α |
| D、若α⊥β,α∥γ,则β⊥γ |
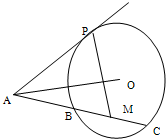 (几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为
(几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为 如图所示,在正三棱柱ABC-A1B1C1中,若AB=2,BB1=
如图所示,在正三棱柱ABC-A1B1C1中,若AB=2,BB1=