题目内容
函数y=sin 2x+cos2(x-
)的单调递增区间是 .
| π |
| 3 |
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:利用降幂公式与两角差的余弦可得y=-
cos2x+
sin2x+1,利用辅助角公式可得y=
sin(2x-
)+1,再由正弦函数的单调性即可求得y=
sin(2x-
)+1的单调增区间.
| 3 |
| 4 |
| ||
| 4 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
解答:
解:∵y=
+
=1-
cos2x+
(cos2xcos
+sin2xsin
)
=-
cos2x+
sin2x+1
=-
(
cos2x-
sin2x)+1
=
sin(2x-
)+1,
由-
+2kπ≤2x-
≤
+2kπ(k∈Z),
得-
+kπ≤x≤
+kπ(k∈Z),
∴y=
sin(2x-
)+1的单调增区间为[-
+kπ,
+kπ](k∈Z).
| 1-cos2x |
| 2 |
1+cos(2x-
| ||
| 2 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
=-
| 3 |
| 4 |
| ||
| 4 |
=-
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得-
| π |
| 12 |
| 5π |
| 12 |
∴y=
| ||
| 2 |
| π |
| 3 |
| π |
| 12 |
| 5π |
| 12 |
点评:本题考查三角函数中的恒等变换应用,考查二倍角公式及正弦函数的单调性,考查转化思想与运算求解能力,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
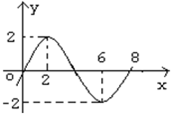 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(11)的值是( )
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(11)的值是( )A、2+2
| ||
B、2-2
| ||
| C、0 | ||
| D、-1 |