题目内容
13.已知圆锥的高为3,底面半径为4,若一球的表面积与此圆锥侧面积相等,则该球的半径为( )| A. | 5 | B. | $\sqrt{5}$ | C. | 9 | D. | 3 |
分析 由已知中圆锥的底面半径和高,求出圆锥的母线长,代入圆锥侧面积公式,求出圆锥侧面积,利用球的表面积与此圆锥侧面积相等,可得答案.
解答 解:∵圆锥的底面半径r=4,高h=3,
∴圆锥的母线l=5,
∴圆锥侧面积S=πrl=20π,
设球的半径为r,则4πr2=20π,∴r=$\sqrt{5}$
故选B.
点评 本题考查的知识点是旋转体,熟练掌握各种旋转体的几何特征,是解答的关键.

练习册系列答案
相关题目
3.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤6}\\{x-3y≤-2}\\{x≥1}\end{array}\right.$若目标函数z=ax+by(a>0,b>0)的最小值为2,则$\frac{1}{a}$+$\frac{3}{b}$的最小值为( )
| A. | 2+$\sqrt{3}$ | B. | 5+2$\sqrt{6}$ | C. | 8+$\sqrt{15}$ | D. | 2$\sqrt{3}$ |
4.若x,y满足不等式$\left\{\begin{array}{l}{x≥2}\\{x+y≤6}\\{x-2y≤0}\end{array}\right.$,则z=x2+y2的最小值是( )
| A. | 2 | B. | $\sqrt{5}$ | C. | 4 | D. | 5 |
1.上饶高铁站B1进站口有3个闸机检票通道口,若某一家庭有3个人检票进站,如果同一个人进的闸机检票通道口选法不同,或几个人进同一个闸机检票通道口但次序不同,都视为不同的进站方式,那么这个家庭3个人的不同进站方式有( )种.
| A. | 24 | B. | 36 | C. | 42 | D. | 60 |
18.已知实数x,y满足不等式组$\left\{\begin{array}{l}{-3≤3x-y≤-1}\\{-1≤x+y≤1}\end{array}\right.$,若z=ax+y有最大值$\frac{5}{2}$,则实数a的值是( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
5.$\frac{3+i}{3-i}$=( )
| A. | $\frac{4}{5}$+$\frac{3}{5}$i | B. | $\frac{4}{5}$-$\frac{3}{5}$i | C. | $\frac{1}{2}$+$\frac{3}{2}$i | D. | $\frac{1}{2}$-$\frac{3}{2}$i |
3.已知集合A={x|-1≤x≤3},B={x|x=2n-1.n∈Z},则A∩B=( )
| A. | {1,3} | B. | {0,2} | C. | {1} | D. | {-1,1,3} |
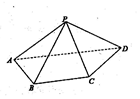 如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.
如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.