题目内容
8.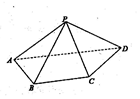 如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.
如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.(1)证明:PC⊥平面PAD;
(2)求直线AB与平面PBC所成的角的大小.
分析 (1)证明PA⊥PC,通过计算求解证明PC⊥PD,然后证明PC⊥平面PAD.
(2)建系 求出相关点的坐标,求出平面PBC的法向量,设直线AB与平面PBC所成的角是θ利用空间向量的数量积求解直线AB与平面PBC所成的角即可.
解答 (1)证明:由已知得:PA⊥PD,PA⊥CD,所以PA⊥平面PCD,即PA⊥PC
在直角梯形ABCD中,AB=1,$AD=2BC=\sqrt{2}$$AC=CD=\frac{{\sqrt{6}}}{2}$,由△PAD是以AD为底边的等腰直角三角形得:AP=PD=1
由PC2+AP2=AC2,得$PC=\frac{{\sqrt{2}}}{2}$,
可算得:PC2+PD2=CD2
所以:PC⊥PD,即PC⊥平面PAD.
(2)如图建系,可得: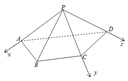
A(1,0,0),$C(0,\frac{{\sqrt{2}}}{2},0)$,D(0,0,1),P(0,0,0)$\overrightarrow{CB}=\frac{1}{2}(1,0,-1)$$\overrightarrow{PC}=(0,\frac{{\sqrt{2}}}{2},0)$,$\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}=(-1,\frac{{\sqrt{2}}}{2},0)+\frac{1}{2}(1,0,-1)=(-\frac{1}{2},\frac{{\sqrt{2}}}{2},-\frac{1}{2})$,
设平面PBC的法向量为$\overrightarrow n=(x,y,z)$,则有$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{CB}=\frac{1}{2}(x-z)=0\\ \overrightarrow n•\overrightarrow{PC}=\frac{{\sqrt{2}}}{2}y=0\end{array}\right.$,令x=1得:$\overrightarrow n=(1,0,1)$,
设直线AB与平面PBC所成的角是θ,∴$sinθ=|cos<\overrightarrow n,\overrightarrow{AB}>|=|\frac{{\overrightarrow n•\overrightarrow{AB}}}{{|\overrightarrow n|•|\overrightarrow{AB}|}}|=|\frac{-1}{{\sqrt{2}}}|=\frac{{\sqrt{2}}}{2}$
所以直线AB与平面PBC所成的角是$\frac{π}{4}$.
点评 本题考查直线与平面所成角的求法,直线与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.

| A. | $[{\frac{e^2}{8},+∞})$ | B. | $({0,\frac{e^3}{27}}]$ | C. | $[{\frac{e^3}{27},+∞})$ | D. | $({0,\frac{e^2}{8}}]$ |
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
| A. | 5 | B. | $\sqrt{5}$ | C. | 9 | D. | 3 |
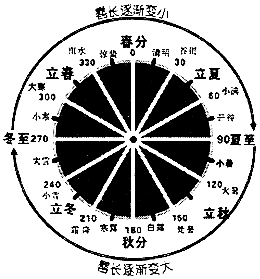 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 四尺五寸 |
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2$\sqrt{3}$ |
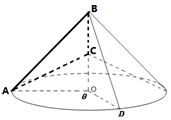 如图,等腰Rt△AOB,OA=OB=2,点C是OB的中点,△AOB绕BO所在的边逆时针旋转一周.
如图,等腰Rt△AOB,OA=OB=2,点C是OB的中点,△AOB绕BO所在的边逆时针旋转一周.