$\frac{3+i}{3-i}$=( )A．$\frac{4}{5}$+$\frac{3}{5}$iB．$\frac{4}{5}$-$\frac{3}{5}$iC．$\frac{1}{2}$+$\frac{3}{2}$iD．$\frac{1}{2}$-$\frac{3}{2}$i 题目和参考答案——青夏教育精英家教网—

题目内容

5．$\frac{3+i}{3-i}$=（　　）

A．

$\frac{4}{5}$+$\frac{3}{5}$i

B．

$\frac{4}{5}$-$\frac{3}{5}$i

C．

$\frac{1}{2}$+$\frac{3}{2}$i

D．

$\frac{1}{2}$-$\frac{3}{2}$i

分析直接利用复数代数形式的乘除运算化简得答案．

解答解：$\frac{3+i}{3-i}$=$\frac{（3+i）^{2}}{（3-i）（3+i）}=\frac{8+6i}{10}=\frac{4}{5}+\frac{3}{5}i$，
故选：A．

点评本题考查复数代数形式的乘除运算，是基础的计算题．

练习册系列答案

16．若存在两个正数x，y，使得等式${x^2}•{e^{\frac{y}{x}}}-2a{y^2}=0$成立，其中e为自然对数的底数，则实数a的取值范围是（　　）

A．

$[{\frac{e^2}{8}，+∞}）$

B．

$（{0，\frac{e^3}{27}}]$

C．

$[{\frac{e^3}{27}，+∞}）$

D．

$（{0，\frac{e^2}{8}}]$

13．已知圆锥的高为3，底面半径为4，若一球的表面积与此圆锥侧面积相等，则该球的半径为（　　）

20．若函数f（x）=sin$\frac{1}{2}$x的图象向左平移φ（φ＞0）个单位得到函数g（x）=cos$\frac{1}{2}$x的图象，则φ的最小值是π．

10．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{2-x}，x＜2}\\{\frac{3}{4}{x}^{2}-3x+4，x≥2}\end{array}\right.$，若不等式a≤f（x）≤b的解集恰好为[a，b]，则b-a=4．

17．

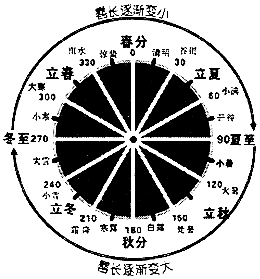我国古代的天文学和数学著作《周髀算经》中记载：一年有二十四个节气，每个节气晷（guǐ）长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度）．二十四节气及晷长变化如图所示，相邻两个节气晷长的变化量相同，周而复始．若冬至晷长一丈三尺五寸，夏至晷长一尺五寸（一丈等于十尺，一尺等于十寸），则夏至之后的那个节气（小暑）晷长是（　　）

14．已知向量$\overrightarrow m=（1，\sqrt{3}sin（wx+\frac{π}{6}）），\overrightarrow n=（2coswx，y）（0＜w＜2）$，且$\overrightarrow m∥\overrightarrow n$，函数y=f（x）的图象过点$（\frac{5π}{12}，\frac{{\sqrt{3}}}{2}）$．
（1）求w的值及函数f（x）的最小正周期；
（2）将y=f（x）的图象向右平移$\frac{π}{6}$个单位，得到函数y=g（x）的图象，已知$g（\frac{α}{2}）=\frac{{5\sqrt{3}}}{6}$，求$cos（2α-\frac{π}{3}）$的值．

15．设实数x，y满足约束条件$\left\{\begin{array}{l}y-x≥0\\ x-2y+2≥0\\ x≥0\end{array}\right.$若目标函数z=mx+y（m＞0）的最大值为6，则m的值为（　　）

试题分类