题目内容
“|x|≥1”是“x≥1”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式之间的关系，结合充分条件和必要条件的定义进行判断即可．
解答：
解：若|x|≥1，则x≥1或x≤-1，
即“|x|≥1”是“x≥1”的必要而不充分条件，
故选：B
即“|x|≥1”是“x≥1”的必要而不充分条件，
故选：B
点评：本题主要考查充分条件和必要条件的判断，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
设m，n是两条不同的直线，α，β是两个不同的平面．（ ）
| A、若m∥α，n?α，则m∥n |
| B、若m⊥α，n?α，则m⊥n |
| C、若α∥β，m?α，n?β，则m∥n |
| D、若α⊥β，m?α，n?β，则m⊥n |
函数y=cosx•ln|x|的部分图象大致是下图中的（ ）
A、 |
B、 |
C、 |
D、 |
若角α的终边落在直线x+y=0上，则
+
的值等于（ ）
| |tanα| |
| tanα |
| sinα | ||||
|
| A、2或-2或0 | B、-2或0 |
| C、2或-2 | D、0或2 |
三次函数f（x）=ax3+2x+5在x∈（-∞，+∞）内是增函数，则（ ）
| A、a＞0 | ||
| B、a＜0 | ||
| C、a=1 | ||
D、a=
|
曲线x2+y2+4x-4y=0关于（ ）
| A、直线x=4对称 |
| B、直线x+y=0对称 |
| C、直线x-y=0对称 |
| D、直线（-4，4）对称 |
把函数y=cosx的图象向左平移
个单位，然后把，图象上的所有点的横坐标缩小到原来的
（纵坐标不变），则所得图形对应的函数解析式为（ ）
| π |
| 4 |
| 1 |
| 2 |
A、y=cos（
| ||||
B、y=cos（2x+
| ||||
C、y=cos（
| ||||
D、y=cos（2x+
|
如图所示是《函数的应用》的知识结构图，如果要加入“用二分法求方程的近似解”，则应该放在（ ）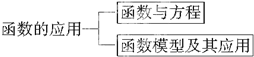
| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |