Question

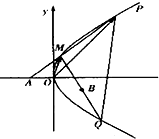已知点A（-1，0），B（1，-1）和抛物线C：y²=4x，O为坐标原点，过点A的动直线l交抛物线C于M、P，直线MB交抛物线C于另一点Q，如图
（1）证明：

OM

•

OP

为定值；
（2）若△POM的面积为

5

2

，求向量

OM

与

OP

的夹角；
（3）证明直线PQ恒过一个定点．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（I）设点M（

y12

4

，y1），P（

y22

4

，y2），由已知条件推导出

y1

y12+4

=

1

y1+y2

，由此能证明

OM

•

OP

为宝值5．
（II）设∠POM=α，则|

OM

|•|

OP

|•cosα=5，由此能求出

OM

与

OP

的夹角．
（Ⅲ）设点Q（

y32

4

，y3），由已知条件推导出y₁y₃+y₁+y₃+4=0，由此能证明直线PQ过定点E（1，-4）．

解答： （I）证明：设点M（

y12

4

，y1），P（

y22

4

，y2），
∵P、M、A三点共线，
∴k_AM=k_PM，即

y1

y1 4 +1

=

y1-y2

y12 4 - y22 4

，
∴

y1

y12+4

=

1

y1+y2

，∴y₁y₂=4，…（2分）
∴

OM

•

OP

=

y12

4

•

y22

4

+y1y2=5．…（5分）
（II）解：设∠POM=α，则|

OM

|•|

OP

|•cosα=5，
∵S_△POM=

5

2

，∴|

OM

|•|

OP

|•sinα=5，
∴tanα=1．…（8分）
又α∈（0，π），∴α∈（0，π），∴α=45°，
∴

OM

与

OP

的夹角为45°．…（10分）
（Ⅲ）证明：设点Q（

y32

4

，y3），∵M、B、Q三点共线，∴k_BQ=k_QM，
∴

y3

y32 4 +1

=

y1-y3

y12 4 - y32 4

，∴

y3+1

y32-4

=

1

y1+y3

，
∴（y₃+1）（y₁+y₃）=y32 -4，即y₁y₃+y₁+y₃+4=0，
∵y₁y₂=4，y1=

4

y2

，∴

4

y2

•y3+

4

y2

+y3+4=0
即4（y₂+y₃）+y₂y₃+4=0，（*）…（12分）
∵k_PQ=

y2-y3

y22 4 - y32 4

=

4

y2+y1

，
∴直线PQ的方程是y-y2=

4

y2+y3

(x-

y22

4

)，
即（y-y₂）（y₂+y₃）=4x-y22，
即y（y₂+y₃）-y₂y₃=4x，
由（*）式，-y₂y₃=4（y₂+y₃）+4，
代入上式，得（y+4）（y₁+y₂）=4（x-1），
∴直线PQ过定点E（1，-4）．

点评：本题考查向量的数量积为定值的证明，考查两向量的夹角的求法，考查直线过定点的证明，解题时要认真审题，注意向量的数量积公式的合理运用．