题目内容
2.以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的方程为$ρsin({θ-\frac{2π}{3}})=-\sqrt{3}$,⊙C的极坐标方程为ρ=4cosθ+2sinθ.(1)求直线l和⊙C的普通方程;
(2)若直线l与圆⊙C交于A,B两点,求弦AB的长.
分析 (1)将$ρsin({θ-\frac{2π}{3}})=-\sqrt{3}$利用和差公式打开;根据x=ρcosθ,y=ρsinθ带入可得直线l和⊙C的普通方程.
(2)利用圆截直线的弦长公式求|AB|即可
解答 解:(1)直线l的方程为$ρsin({θ-\frac{2π}{3}})=-\sqrt{3}$,
可得:ρsinθcos$\frac{2π}{3}$-ρcosθsin$\frac{2π}{3}$=-$\sqrt{3}$
?-$\frac{1}{2}$y-$\frac{\sqrt{3}}{2}$x=$-\sqrt{3}$
即:$\sqrt{3}x+y=2\sqrt{3}$.
⊙C的极坐标方程为ρ=4cosθ+2sinθ.
可得:ρ2=4ρcosθ+2ρsinθ,
?x2+y2=4x+2y
即:x2+y2-4x-2y=0,
故得直线l的普通方程为:$\sqrt{3}x+y=2\sqrt{3}$;⊙C的普通方程为:x2+y2-4x-2y=0.
(2)由x2+y2-4x-2y=0,可知圆心为(2,1),半径r=$\sqrt{5}$,
那么:圆心到直线的距离d=$\frac{|2\sqrt{3}+1-2\sqrt{3}|}{2}=\frac{1}{2}$,
∴|AB|=2$\sqrt{{r}^{2}-{d}^{2}}=\sqrt{19}$
故得直线l与圆⊙C交于A,B两点间的弦AB长为$\sqrt{19}$.
点评 本题主要考查了极坐标方程与直角坐标方程的互换和圆心到直线的距离公式的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
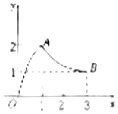 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.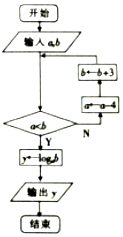 如图是一个算法的流程图,当输入a=10,b=2的时,输出的y值为3.
如图是一个算法的流程图,当输入a=10,b=2的时,输出的y值为3.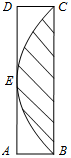 如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.
如图所示矩形ABCD边长AB=1,AD=4,抛物线顶点为边AD的中点E,且B,C两点在抛物线上,则从矩形内任取一点落在抛物线与边BC围成的封闭区域(包含边界上的点)内的概率是$\frac{2}{3}$.