题目内容
17.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且经过点(0,1).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知直线l:y=kx+m(k≠0)与椭圆C相交于A,B两点,若以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
分析 (Ⅰ)由已知求得b,结合离心率及隐含条件求得a,则椭圆方程可求;
(Ⅱ)联立直线方程和椭圆方程,化为关于x的一元二次方程,利用根与系数的关系求得两点横纵坐标的乘积,再由向量数量积为0求得m与k的关系,分类求出直线方程可得直线l过定点的坐标.
解答 解:(Ⅰ)∵点(0,1)在椭圆上,∴b2=1,即b=1.
∵$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,∴$\frac{{{a^2}-1}}{a^2}=\frac{3}{4}$,解得a=2.
∴椭圆的标准方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)设A(x1,y1),B(x2,y2),
由$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{4}+{y^2}=1}\end{array}}\right.$,得(1+4k2)x2+8mkx+4(m2-1)=0,
△=64m2k2-16(1+4k2)(m2-1)>0,即1+4k2-m2>0.
${x}_{1}+{x}_{2}=\frac{-8km}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4({m}^{2}-1)}{1+4{k}^{2}}$.
${y_1}•{y_2}=(k{x_1}+m)•(k{x_2}+m)={k^2}{x_1}{x_2}+mk({x_1}+{x_2})+{m^2}=\frac{{{m^2}-4{k^2}}}{{1+4{k^2}}}$.
∵以AB为直径的圆过椭圆的右顶点D(2,0),∴AD⊥BD,
∴$\overrightarrow{AD}•\overrightarrow{BD}=0$,
∵$\overrightarrow{AD}=(2-{x_1},-{y_1}),\overrightarrow{BD}=(2-{x_2},-{y_2})$,
∴x1x2-2(x1+x2)+4+y1y2=0,即$\frac{{4({m^2}-1)}}{{1+4{k^2}}}+\frac{16mk}{{1+4{k^2}}}+4+\frac{{{m^2}-4{k^2}}}{{1+4{k^2}}}=0$,
即5m2+16mk+12k2=0,解得:${m_1}=-2k,{m_2}=-\frac{6k}{5}$,且满足1+4k2-m2>0.
当m=-2k时,l:y=k(x-2),直线过定点(2,0),与已知矛盾;
当$m=-\frac{6k}{5}$时,$l:y=k(x-\frac{6}{5})$,直线过定点$(\frac{6}{5},0)$.
综上可知,直线l过定点,定点坐标为$(\frac{6}{5},0)$.
点评 本题考查椭圆标准方程的求法,考查椭圆的简单性质,训练了直线与椭圆位置关系的应用,属中档题.

| A. | 等边三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形但不是等腰三角形 | D. | 等腰三角形但不是直角三角形 |
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{5}{4}$ | D. | $\frac{5}{3}$或$\frac{5}{3}$ |
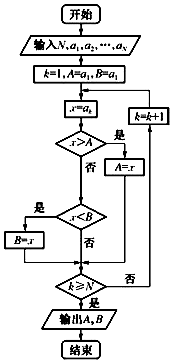 如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )| A. | A+B为a1,a2,…,aN的和 | |
| B. | A和B分别是a1,a2,…,aN中最大的数和最小的数 | |
| C. | $\frac{A+B}{2}$为a1,a2,…,aN的算术平均数 | |
| D. | A和B分别是a1,a2,…,aN中最小的数和最大的数 |