题目内容
14.已知函数$f(x)=\sqrt{3}sin2x-2{cos^2}x$.(1)若$β∈[{0,\frac{π}{2}}]$,求f(β)的取值范围;
(2)若$tanα=2\sqrt{3}$,求f(α)的值.
分析 (1)利用二倍角和辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,结合三角函数的图象和性质,得到f(x)的取值范围.
(2)已知$tanα=2\sqrt{3}$,求解f(α)的表达式,构造正切.可得结论.
解答 解:函数$f(x)=\sqrt{3}sin2x-2{cos^2}x$.
化简可得:f(x)=$\sqrt{3}$sin2x-cos2x-1
=2sin(2x-$\frac{π}{6}$)-1
那么:f(β)=2sin(2β$-\frac{π}{6}$)-1
∵$β∈[{0,\frac{π}{2}}]$,
∴2β$-\frac{π}{6}$∈[$-\frac{π}{6},\frac{5π}{6}$],
∴sin(2β$-\frac{π}{6}$)∈[$-\frac{1}{2}$,1]
故得f(β)的取值范围是[-2,1]
(2)函数$f(x)=\sqrt{3}sin2x-2{cos^2}x$.
那么:f(α)=$\sqrt{3}$sin2α-2cos2α=$\frac{2\sqrt{3}sinαcosα-2co{s}^{2}α}{si{n}^{2}α+co{s}^{2}α}=\frac{2\sqrt{3}tanα-2}{ta{n}^{2}α+1}$
∵$tanα=2\sqrt{3}$,
∴f(α)=$\frac{2\sqrt{3}×2\sqrt{3}-2}{4×3+1}=\frac{10}{13}$.
点评 本题主要考查对三角函数的化简能力,函数性质和同角三角函数关系式的计算.属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
5.与双曲线$C:\frac{x^2}{16}-\frac{y^2}{9}=1$有相同的渐近线的双曲线E的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$或$\frac{5}{4}$ | D. | $\frac{5}{3}$或$\frac{5}{3}$ |
6.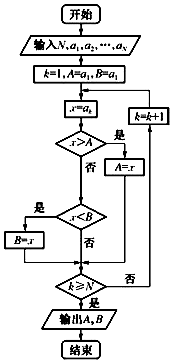 如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
 如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
如果执行如图所示的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )| A. | A+B为a1,a2,…,aN的和 | |
| B. | A和B分别是a1,a2,…,aN中最大的数和最小的数 | |
| C. | $\frac{A+B}{2}$为a1,a2,…,aN的算术平均数 | |
| D. | A和B分别是a1,a2,…,aN中最小的数和最大的数 |
3.已知f(x)是奇函数,当x>0时,f(x)=1gx,设a=f(3),b=$f(\frac{1}{4})$,c=f(-2),则( )
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | b>a>c |
4.设数列{an}的前n项和为Sn,已知a2=2,an+2+(-1)n-1an=1,则S40=( )
| A. | 260 | B. | 250 | C. | 240 | D. | 230 |