题目内容

12．?x∈R，使得x2-mx+1≤0成立，则实数m的取值范围为m≥2或m≤-2．

分析 若?x∈R，使得x2-mx+1≤0成立，则△=m2-4≥0，解得实数m的取值范围．

解答 解：若?x∈R，使得x2-mx+1≤0成立，
则△=m2-4≥0，
解得：m≥2或m≤-2，
故答案为：m≥2或m≤-2

点评 本题以命题的真假判断与应用为载体，考查了特称命题，二次函数的图象和性质，难度基础．

练习册系列答案
相关题目
2．以原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的方程为$ρsin（{θ-\frac{2π}{3}}）=-\sqrt{3}$，⊙C的极坐标方程为ρ=4cosθ+2sinθ．
（1）求直线l和⊙C的普通方程；
（2）若直线l与圆⊙C交于A，B两点，求弦AB的长．
3．已知f（x）是奇函数，当x＞0时，f（x）=1gx，设a=f（3），b=$f（\frac{1}{4}）$，c=f（-2），则（　　）
A．a＞c＞bB．a＞b＞cC．c＞a＞bD．b＞a＞c
20．已知数列{an}的前n项和为Sn，且${S_n}={a_n}+{n^2}-1（{n∈{N^*}}）$．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）定义x=[x]+＜x＞，其中[x]为实数x的整数部分，＜x＞为x的小数部分，且0≤＜x＞＜1，记cn=＜$\frac{{{a_n}{a_{n+1}}}}{S_n}$＞，求数列{cn}的前n项和Tn．
7．已知$f（x）=\left\{{\begin{array}{l}{f（x+1），}&{x＜2}\\{{2^x}，}&{x≥2}\end{array}}\right.$，则f（log23）=（　　）
A．12B．6C．4D．2
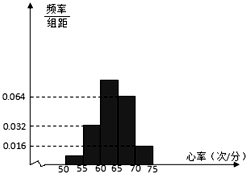17．某高校要了解在校学生的身体健康状况，随机抽取了50名学生进行心率测试，心率全部介于50次/分到75次/分之间，现将数据分成五组，第一组[50，55），第二组[55，60）…第五组[70，75]，按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前三组的频率之比为a：4：10．
（1）求a的值．
（2）若从第一、第五组两组数据中随机抽取两名学生的心率，求这两个心率之差的绝对值大于5的概率．
4．设数列{an}的前n项和为Sn，已知a2=2，an+2+（-1）n-1an=1，则S40=（　　）
A．260B．250C．240D．230
1．在△ABC中，a=$\sqrt{3}$，b=1，∠A=$\frac{π}{3}$，则cosB=$\frac{\sqrt{3}}{2}$．
2．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知3b=4c，B=2C．
（Ⅰ）求sinB的值；
（Ⅱ）若b=4，求△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网