题目内容
已知数列{an}中，a1=1，an+1=an+3，若an=2014，则n=（ ）
| A、667 | B、668 |
| C、669 | D、672 |
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：直接利用等差数列的通项公式得答案．
解答：
解：∵a1=1，an+1=an+3，
∴an+1-an=3，
∴{an}为首项a1=1公差d=3的等差数列，
∴an=a1+（n-1）d=3n-2．
∵an=2 014，
∴3n-2=2014，解得：n=672．
故选：D．
∴an+1-an=3，
∴{an}为首项a1=1公差d=3的等差数列，
∴an=a1+（n-1）d=3n-2．
∵an=2 014，
∴3n-2=2014，解得：n=672．
故选：D．
点评：本题考查了等差数列的通项公式，是基础的计算题．
练习册系列答案
相关题目
如果命题“￢（p∨q）”是假命题，则下列说法正确的是（ ）
| A、p、q均为真命题 |
| B、p、q中至少有一个为真命题 |
| C、p、q均为假命题 |
| D、p、q中至少有一个为假命题 |
已知集合A={x|y=lg（2x-x2）}，B={y|y=2x，x＞0}，R是实数集，则（∁RB）∩A=（ ）
| A、（0，1] |
| B、[0，1] |
| C、（-∞，0] |
| D、以上都不对 |
复数z满足|z+i|=zi，则z的共轭复数
为（ ）
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知{1，2，3}，B={2，4}，定义A-B={x|x∈A且x∉B}，则A-B=（ ）
| A、{1，2，3} |
| B、{2，4} |
| C、{1，3} |
| D、{2} |
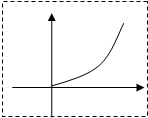已知定义在[0，1]上的函数y=f（x）图象如图所示，且f（1）=1，则对满足0＜x1＜x2＜1的任意x1，x2，下列关系：（1）f（x1）＜x1，（2）x1+f（x2）＜x2+f（x1），（3）x2f（x1）＜x1f（x2）其中一定正确的是