题目内容
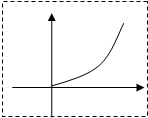已知定义在[0，1]上的函数y=f（x）图象如图所示，且f（1）=1，则对满足0＜x1＜x2＜1的任意x1，x2，下列关系：（1）f（x1）＜x1，（2）x1+f（x2）＜x2+f（x1），（3）x2f（x1）＜x1f（x2）其中一定正确的是考点：函数单调性的性质
专题：函数的性质及应用
分析：由函数的图象，我们可根据图象上任意两点与原点连线的斜率的大小判断（1）正确，图象上任意两点之间的斜率与1的大小判断（2）（3）的对错．
解答：
解：（1）由f（x1）＜x1，得
＜1，
即两点（x1，f（x1））与（0，0）连线的斜率小于1，显然正确；
（2）由x1+f（x2）＜x2+f（x1），得：
＜1，
即两点（x1，f（x1））与（x2，f（x2））连线的斜率小于1，显然错误；
（3）由x2f（x1）＜x1f（x2），得：
＜
，
即表示两点（x1，f（x1））、（x2，f（x2））与原点连线的斜率的大小，显然正确；
故答案为：（1），（3）．
| f(x1) |
| x1 |
即两点（x1，f（x1））与（0，0）连线的斜率小于1，显然正确；
（2）由x1+f（x2）＜x2+f（x1），得：
| f(x2)-f(x1) |
| x2-x1 |
即两点（x1，f（x1））与（x2，f（x2））连线的斜率小于1，显然错误；
（3）由x2f（x1）＜x1f（x2），得：
| f(x1) |
| x1 |
| f(x2) |
| x2 |
即表示两点（x1，f（x1））、（x2，f（x2））与原点连线的斜率的大小，显然正确；
故答案为：（1），（3）．
点评：本题考查的知识点是函数的图象和直线的斜率，解答的关键是结合函数图象分析结论中式子的几何意义，然后进行判断．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知数列{an}中，a1=1，an+1=an+3，若an=2014，则n=（ ）
| A、667 | B、668 |
| C、669 | D、672 |
在（0，2π）内，使|sinx|≥cosx成立的x的取值范围为（ ）
A、[
| ||||
B、[
| ||||
C、[0，
| ||||
D、[0，
|
命题“存在x0∈R，2 x0≤0”的否定是（ ）
| A、不存在x0∈R，2 x0＞0 |
| B、存在x0∈R，2 x0≥0 |
| C、对任意的x∈R，2x≤0 |
| D、对任意的x∈R，2x＞0 |
若关于x的方程4x+m•2x+1+m2-m-2=0有解，则实数m的取值范围是（ ）
| A、[-2，-1） |
| B、[-2，0） |
| C、[-2，2） |
| D、[-2，+∞） |
已知底面边长为
，侧棱长为6的正四棱柱的各顶点均在同一个球面上，其对角线为直径，则该球的体积为（ ）
| 3 |
A、
| ||
B、7
| ||
C、
| ||
D、
|