题目内容
3.某四棱锥的三视图如图所示,该四棱锥外接球的表面积为( )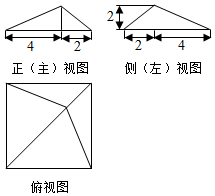
| A. | 72π | B. | 100π | C. | 108π | D. | 72$\sqrt{2}π$ |
分析 作出棱锥的直观图,根据三视图数据可知过底面对角线的平面即为外接球大圆,利用平面几何解出大圆的半径.
解答 解:根据三视图作出四棱锥的直观图如图所示: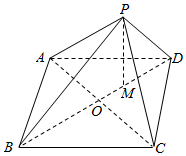
由三视图可知,四棱锥的底面ABCD是边长为6的正方形,P在底面的射影M在底面对角线BD上,
PM=2,且$\frac{DM}{BM}=\frac{1}{2}$.∴OB=3$\sqrt{2}$,设底面中心为O,则OM=$\sqrt{2}$,
∴平面BDP即为四棱锥外接球的大圆所在平面.作出该大圆的截面如图: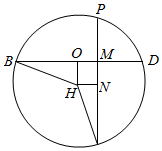
设外接球球心为H,过H作BD的垂线HO,PM的垂线HN,则HN=OM=$\sqrt{2}$,
设大圆半径为R,则MN=OH=$\sqrt{{R}^{2}-O{B}^{2}}$=$\sqrt{{R}^{2}-18}$,PN=$\sqrt{H{P}^{2}-H{N}^{2}}$=$\sqrt{{R}^{2}-2}$.
∵PM=PN-MN,∴$\sqrt{{R}^{2}-2}$-$\sqrt{{R}^{2}-18}$=2.解得R=$\sqrt{27}$.
外接球的表面积S=4πR2=108π.
故选C.
点评 本题考查了棱锥的三视图,棱锥与外接球的关系,寻找大圆截面是解题关键.

练习册系列答案
相关题目
15.下列关系正确的是( )
| A. | 0∉N | B. | $0•\overrightarrow{AB}=0$ | C. | cos0.75°>cos0.7 | D. | lge>(lge)2>lg$\sqrt{e}$ |